Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 25
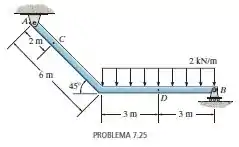
Determine as forças normal e cortante e o momento fletor nos pontos e .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Vamos começar desenhando o nosso D.C.L do membro AB.
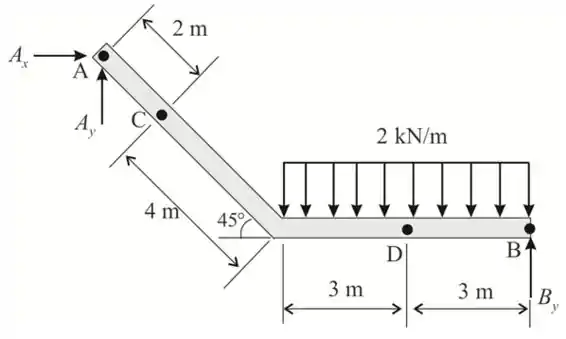
Passo 2
Agora iremos tomar o momento sobre A
Da equação de equilíbrio ao longo do eixo x.
Da equação de equilíbrio ao longo do eixo y
Passo 3
Agora iremos considerar o pedaço AC.
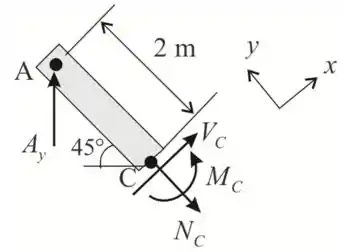
Passo 4
Da equação de equilíbrio ao longo de x,
Portanto a força cortante no ponto C é de .
Da equação de equilíbrio ao longo do eixo de y
Portanto a força normal no ponto C é de
Tomando o momento sobre C
Portanto, o momento sobre o ponto C é de
Passo 5
Agora iremos analisar BD
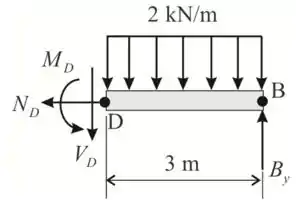
Passo 6
Da equação de equilíbrio ao longo de y,
Portanto a força cortante no ponto D é de .
Da equação de equilíbrio ao longo do eixo de x
Portanto a força normal no ponto D é .
Tomando o momento sobre D
Portanto, o momento sobre o ponto D é de