Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 122
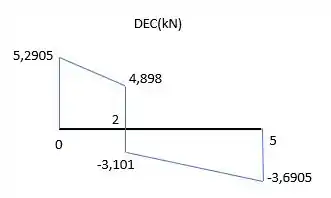
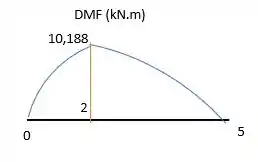
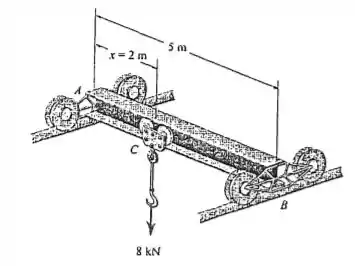
A ponte rolante consiste em uma viga de com uma massa uniforme por unidade de comprimento de . O gancho suspenso e sua carga suportada exercem uma força de na viga quando . Determine os diagramas de esforço cortante e momento fletor para a viga. As rodas-guia nas extremidades exercem apenas reações verticais sobre a viga. Despreze a dimensão do carrinho em .
Passo 1
Cara, o desenho está em 3D, mas ela super pode ser entendida como uma viga com cargas no plano.
Ele diz que ela tem uma massa com distribuição uniforme . Se a gente multiplicar pela gravidade, isso vira uma distribuição de peso. Aí a gente pode entender essa distribuição como uma carga distribuída de valor .
Temos também as reações em e , e força pontual para baixo de
Aí o DCL ficaria:
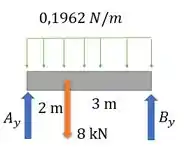
Desejamos traçar os diagramas de esforço cortante e momento fletor para a nossa viga. Assim, vamos calcular antes o valor de todas as forças que atuam nessa viga e que nos são possíveis de serem calculadas de tal forma que nosso cálculo fique simplificado. Dessa forma, façamos primeiramente as reações de suporte
Passo 2
Vamos traçar nossas equações para esses esforços. Devido a força concentrada, teremos duas equações para cada esforço.
Nós vamos cortar nossa viga na seção dentro do intervalo em questão, olhar só para um dos lados, e colocar as componentes dos esforços internos na seção seguindo a convenção dos valores positivos. Aí achamos as equações usando as equações de equilíbrio. Assim:
Para
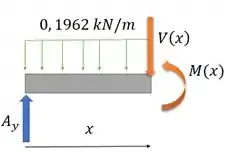
Passo 3
Agora, para temos
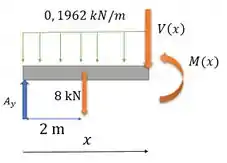
Passo 4
Plotando essas curvas, vamos ter:
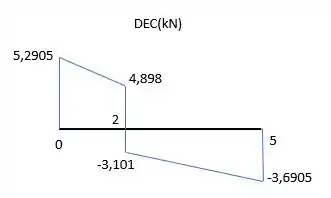
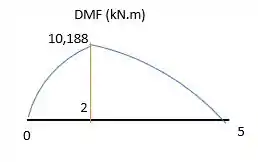
Resposta
