Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 126
A viga uniforme pesa e é mantida na posição horizontal por meio do cabo , que tem um peso de Se a inclinação do cabo em é , determine o comprimento do cabo.
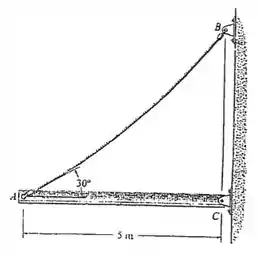
Passo 1
Desejamos encontrar o comprimento do cabo e, para isso, devemos lembrar que como o peso do cabo é de podemos concentrá-lo no meio da barra desde que façamos a seguinte operação : . Dessa forma, podemos traçar o seguinte diagrama de forças para a barra
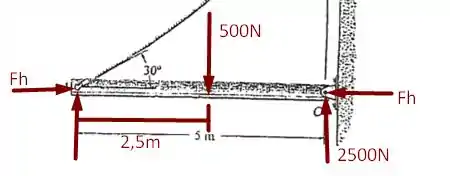
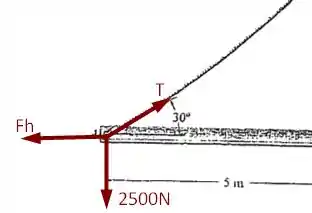
Já para a extremidade do cabo em teremos uma tração assim, vamos ter o seguinte diagrama de forças
Passo 2
Dadas as figuras acima, conseguimos de maneira fazendo o equilíbrio de forças
Além disso, também podemos fazer
Da geometria do problema podemos fazer a seguinte construção com relação a taxa de variação de em relação a
Quando temos que . Substituindo essa informação em
O comprimento do nosso cabo vai ser dado por
Temos que em
Portanto, teremos quando