Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 23
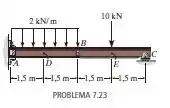
Determine as forças normal e cortante e o momento fletor nos pontos e na viga composta de dois elementos. O ponto está localizado logo à esquerda da carga concentrada de . Considere o apoio em um engastamento e a conexão em um pino.
Passo 1
E aí... belezinha???
Nessa questão vamos usar as equações de equilíbrio:
- Somatório das forças em :
- em :
- e pro momento:
Ahhhh... Repara que temos um engastamento em , um pino em e um rolete em ... Se a gente fizer o equilíbrio nessa barra toda vai ter 3 reações em , 2 em e uma em . Ou seja, 6 incógnitas para 3 equações de equilíbrio. Daí não daria pra resolver.
A nossa saída, então, é dividir a barra em duas partes: segmento de até e de até .
Passo 2
Começando pelo que possivelmente deve dar menos trabalho... O segmente :
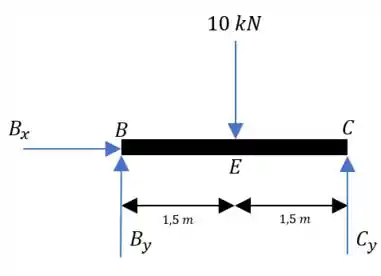
Fazendo o somatório das forças em :
Em :
E para o momento:
Daí também:
Passo 3
Fazendo o corte em :
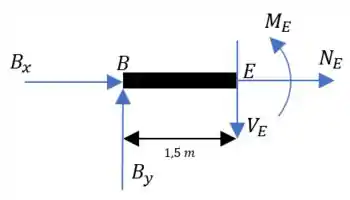
Uma suuuuuuper atenção aqui porque a carga de não entre nesse corte porque o enunciado disse que o ponto está logo à esquerda da carga concentrada.
Fazendo o somatório das forças em :
Em :
E para o momento:
Ohhhhh... uma parte já foi, heim!? Bora continuar que falta pouco...
Passo 4
Como a gente já tem as reações no ponto que tal usarmos o segmento ?? (Já que não foi pedido pra calcular nenhuma das três reações no ponto )
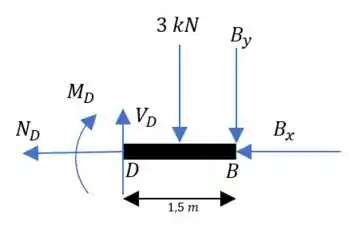
Fazendo o somatório em :
Em :
E para o momento:
Ufa... acabamos. Bora pra próxima?