Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 128
Determine as forças que os pinos e exercem sobre a estrutura de dois membros sustentando a caixa de .
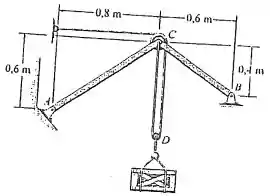
Passo 1
Para determinar as forças, deve-se fazer o diagrama de corpo livre no qual sejam indicadas todas as forças atuando na estrutura.
Neste caso, deve-se perceber que a força peso gerada pela caixa é dividida igualmente entre as duas cordas que saem da polia em .
Então, fazendo o DCL, tem-se que:
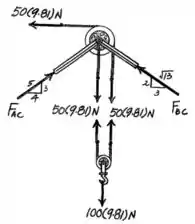
Passo 2
Logo, para determinar as forças que agem sobre os pinos e é suficiente realizar o equilíbrio de forças nos dois eixos coordenados horizontal e vertical pelo fato de ambas as forças terem componentes nesses eixos. Assim, haverá duas variáveis e duas equações a serem resolvidas.
Além disso, como a caixa está sendo sustentada pelo sistema, o mesmo está em equilíbrio.
Passo 3
Sendo assim, fazendo o equilíbrio de forças em :
E fazendo o equilíbrio de forças em , tem-se que:
Passo 4
Com as equações (1) e (2) é possível resolver um sistema de equações que nos dará como solução os valores das forças exercidas em e que são dados por: