Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 2
Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Passo 1
Beleza! A primeira coisa que devemos fazer é desenhar o diagrama de corpo livre da treliça:
Agora aplicando o somatório de forças na direção :
Agora, aplicando o somatório de momento com relação ao ponto , temos:
Isolando temos:
Agora aplicando o somatório de forças na direção :
Isolando :
Passo 2
Agora vamos analisar o nó B:
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:
Então, pegando a primeira e terceira parcelas:
Agora pegando a segunda e terceira parcelas:
Passo 3
Agora vamos analisar o nó C:
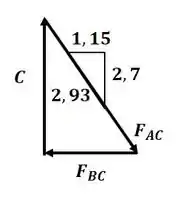
Aplicando semelhança de triângulos entre o triângulo de forças e o de comprimento, temos:
Isolando :
Passo 4
Resposta
Ei, a resposta está no passo a passo :)