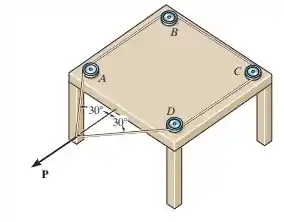
3.34. O fio forma um contorno fechado e passa pelas pequenas polias em A, B, C e D. Se a força resultante máxima que o fio pode exercer sobre cada polia é , determine a maior força P que pode ser aplicada ao fio como mostrado.
Passo 1
Fala aai galerinha bonita, tudo beleza?! Saca só, o enunciado nos disse que uma força atua sobre uma mesa através de cabos que passam por polias como na figura abaixo:
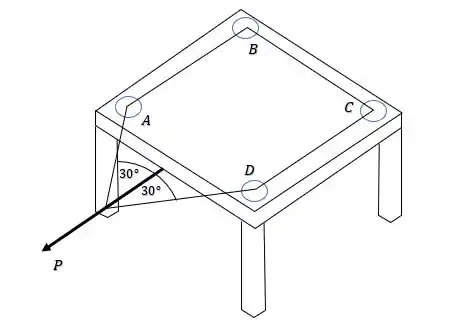
Sabendo que a carga máxima que um cabo pode exercer sobre uma polia é de , o enunciado quer que a gente descubra o maior valor possível para para que o sistema continue em equilíbrio.
Belezoca então pessoal, como o sistema deve estar em equilíbrio, quer dizer que o somatório das forças que atuam sobre ele deve ser nulo. E podemos analisar as forças que atuam através do ponto de contato entre e os cabos, como no diagrama a seguir:
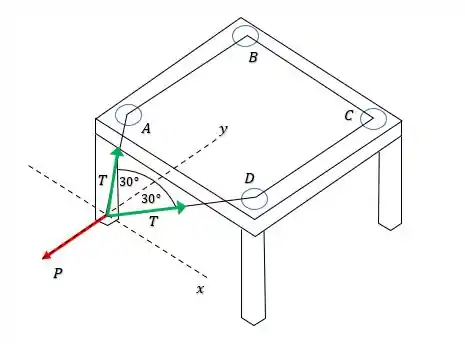
Onde representa a tensão no cabo. Iradoso, agora podemos usar as equações de equilíbrio para os eixos.
Passo 2
Vamos usar as condições de equilíbrio para o eixo , teremos que:
Logo:
Isolando , descobrimos que:
Passo 3
Maravilha, mas agora que vem a malandragem toda.

Porque lembra que o enunciado nos disse que a força resultante máxima que um cabo pode exercer sobre uma polia é de ?! Então, essa força resultante máxima fica mais tranquilo da gente enxergar quando ocorre nas polias e :
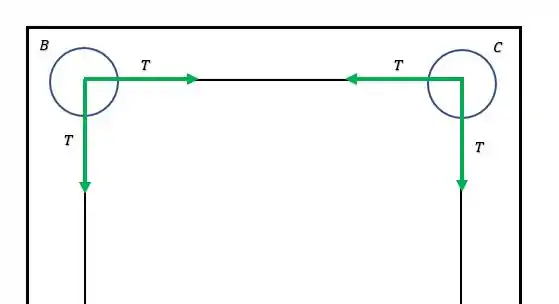
Ou seja, a força resultante que ocorre nas polias e são dadas como:
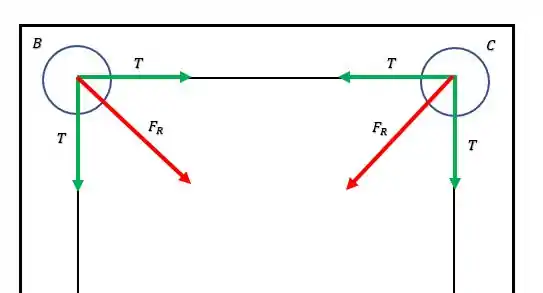
Isso quer dizer que podemos calcular o força resultante através da relação:
E como vimos que e , vamos ter que:
Logo:
Isolando vamos chegar que:
