Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 34
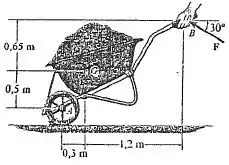
34. A fim de manter o carrinho de mão na posição indicada, a força de produzir um momento anti-horário de em relação a o eixo A. Determine a intensidade necessária da força .
Passo 1
Para resolver exercício temos que usar o princípio dos momentos.
Nossa força aplicada pode ser dividida em duas componentes em relação a eixo cartesiano e essas duas forças vão ter momento associado a elas.
Uma das componentes vai ser em e a outra em , então basta multiplicar cada força por seu braço de momento correspondente.
E a soma do momento de cada componente vai ser igual ao momento do total. Então como o enunciado já dá o valor do momento total, basta isolar o e assim achar o que o enunciado pede.
Passo 2
Vamos agora calcular a componente de cada força.
A componente em é dada por:
A componente em é dado por:
Passo 3
Agora calculando o momento de cada força:
Primeiro para componente :
Agora vamos calcular para componente :
Então o momento total é dado pela soma desses dois momentos encontrados, logo:
Passo 4
O enunciado nos forneceu o momento total que é . Assim ficamos com:
Resposta
A intensidade necessária da força é .