Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 101

Determine as intensidades dos momentos de binário M 1 , M 2 e M 3 de modo que o momento de binário resultante seja zero.

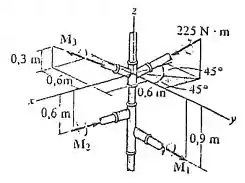
Passo 1

Fala aí gurizada, tudo belezinha? Como temos um vetor livre ele pode agir a qualquer momento sem alterar seu efeito, assim os momentos M 1 , M 2 e M 3 e M4 podem ser simplificados da seguinte maneira, vem comigo!!

M 1 → = M 1 j ^

M 2 → = - M 2 i ^

M 3 → = ? ? ?

M 4 → = ? ? ?

Vamos encontrar o M 3 →   e   o   M 4 → gurizada, vem comigo!!

Para o binário M 3 , note que ele está na direção do vetor ( 0,6 ;   - 0,6 ; 0,3 ) que é a mesma direção do vetor ( 2 ,   - 2 ,   1 ) , Então, teremos:

M 3 → = M 3   2 - 0 i + - 2 - 0 j + 1 + 0 K 2 - 0 2 + - 2 - 0 2 + ( 1 - 0 ) ² 2 3   i ^ - 2 3   j ^ + 1 3 k ^

M 3 → = M 3   2 3   i ^ - 2 3   j ^ + 1 3 k ^

Agora partiu achar M4

M 4 → = - M cos ⁡ 45 °   k ^ + M   s e n   45 °   cos ⁡ 45 °   i ^ - s e n   45 °   j ^ ,

com M = 225   N ⋅ m . Desta forma, temos que

M 4 → = M   1 2   i ^ - 1 2   j ^ - 2 2   k ^

Passo 2

O binário resultante será dado por:

M → = M 1 → + M 2 → + M 3 → + M 4 →

Assim, teremos:

M → = - M 2 + 2 M 3 3 + M 2 i ^ + M 1 - 2 M 3 3 - M 2 j ^ + M 3 - M 2 2 k ^

Como queremos que o binário resultante seja nulo, temos que impor que cada componente se anula:

Partiu fazer sisteminha!!!

- M 2 + 2 M 3 3 + M 2 = 0 M 1 - 2 M 3 3 - M 2 = 0 M 3 3 - M 2 2 = 0

Passo 3

Da última equação, tiramos que:

M 3 = 3 M 2 2 = 3 M 2

Substituindo isso na segunda equação:

M 1 - 2 3 ⋅ 3 M 2 - M 2 = 0 ⇒ M 1 = M   1 2 + 2

E na primeira:

- M 2 + 2 3 ⋅ 3 M 2 + M 2 = 0 ⇒ M 2 = M 1 2 + 2

Usando M = 225   N ⋅ m , obtemos

M 1 = M 2 = 430,7   N ⋅ m           e             M 3 = 477,3   N ⋅ m

Resposta

M 1 = M 2 = 430,7   N ⋅ m           e             M 3 = 477,3   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o torsor geralmente pode ser substituído por duas forças escolhidas de tal modo que uma força passa por um dado ponto enquanto a outra fica em um dado plano.
Substitua o torsor mostrado na figura por um sistema equivalente que consista em duas forças perpendiculares ao eixo y exercidas, respectivamente, em A e B ..
Duas cordas amarradas em A e B são usadas para mover um tronco de uma árvore caída. Substitua as forças exercidas pelas cordas por um torsor equivalente e determine a a resultante R , b o passo do tor
Determine se o sistema de forças e binários mostrado na figura pode ser reduzido a uma força única equivalente R . Se for o caso, determine R e o ponto em que a linha de ação de R intercepta o plano y
Determine se o sistema de forças e binários mostrado na figura pode ser reduzido a uma força única equivalente R . Se for o caso, determine R e o ponto em que a linha de ação de R intercepta o plano y