Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 6

Determine o intervalo de valores de P para o qual o equilíbrio do bloco mostrado na figura é mantido.

Passo 1

Tá legal! Vamos começar o exercício analisando o caso onde o bloco está tendendo a deslizar no sentido iminente de movimento, que seria para baixo, então, o DCL nesse caso será:

Com o DCL, e lembrando da fórmula apresentada nessa seção, podemos calcular o valor de :

Agora, desenhando o triângulo de forças do sistema:

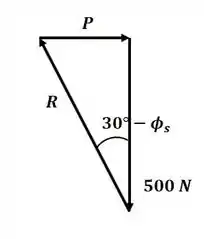
Conseguimos calcular o valor da força P através de:

Isolando e substituindo o valor de encontrado, temos:

Passo 2

Agora vamos repetir o processo, mas analisando o caso onde o bloco está na iminência de se mover para cima, então o DCL será:

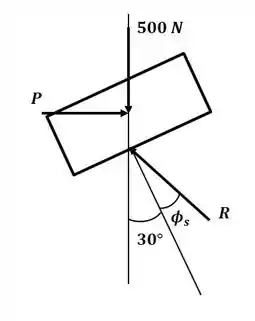
Com o DCL, e lembrando da fórmula apresentada nessa seção, podemos calcular o valor de :

Agora, desenhando o triângulo de forças do sistema:

Conseguimos calcular o valor da força P através de:

Isolando e substituindo o valor de encontrado, temos:

Passo 3

Dessa forma, o intervalo de deve ser:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um momento anti-horário M = 1500 lb-in. é aplicado ao volante. Se o coeficiente de atrito entre a banda e a roda for 0,20, calcule a força mínima P necessária para evitar que a roda gire

Um bloco B de 12 lb repousa, tal como mostra a figura, sobre a superfície superior de uma cunha A de 30 lb. Desprezando o atrito, determine, imediatamente depois que o sistema é solto a partir do repo

O invólucro semicilíndrico de massa me raio r é enrolado através de um ângulo θ pela força P que permanece tangente à sua periferia em A, como mostrado. Se P for aumentado lentamente, plote o ângulo d

Mostre que o momento angular por unidade de massa h de um satélite que descreve uma órbita elíptica de semieixo maior a e excentricidade ε , em torno de um planeta de massa M, pode ser expresso como h

O pólo esbelto uniforme repousa contra um pequeno rolo em B. A extremidade A não escorregará na superfície horizontal se o coeficiente de atrito estático μs for suficientemente grande. (a) Determine o