Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 10

O bloco de 360 N está ligado à articulação AB e repousa sobre uma esteira em movimento. Sabendo que e determine a intensidade da força horizontal que pode ser aplicada na esteira para manter esse movimento para a direita, para a esquerda.

Passo 1

Tá legal! Vamos começar o exercício desenhando o DCL do sistema para quando o movimento ocorre para a direita:

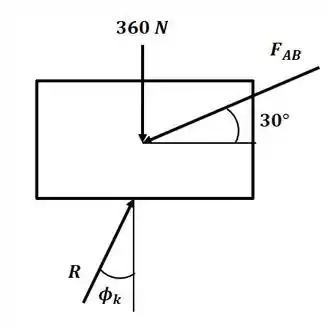
Com o DCL, e lembrando da fórmula apresentada nessa seção, podemos calcular o valor de :

Passo 2

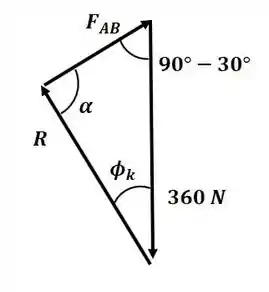
Agora vamos desenhar o triângulo de forças para o sistema:

Nesse triângulo, podemos aplicar a lei dos senos para encontrar o valor de , mas para isso, precisamos do valor de , que pode ser encontrado pela soma dos ângulos internos do triângulo:

Então, aplicando a lei dos senos:

Agora, com o valor da reação R, podemos desenhar o DCL para a esteira e encontrar o valor de :

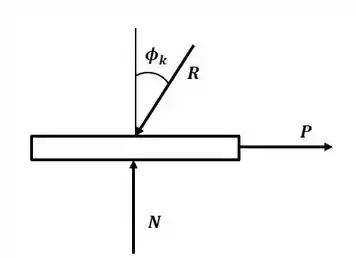
Aplicando o somatório de forças na direção :

Passo 3

Agora, vamos analisar o DCL do sistema para quando o movimento ocorre para a esquerda:

Como permanece o mesmo, podemos desenhar o triângulo de forças para o sistema:

Nesse triângulo, podemos aplicar a lei dos senos para encontrar o valor de , mas para isso, precisamos do valor de , que pode ser encontrado pela soma dos ângulos internos do triângulo:

Então, aplicando a lei dos senos:

Agora, com o valor da reação R, podemos desenhar o DCL para a esteira e encontrar o valor de :

Aplicando o somatório de forças na direção :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/1) A força P é aplicada ao caixote de 90k g , que está em repouso antes que ela seja aplicada . Determine o módulo e a direção da força de atrito F exercida pela superfície horizontal sobre o caixot

6/13) Uma pessoa ( massa m 1 ) ajoelhada em um painel de compensado (massa m 2 ) deseja se empurrar e ao painel para loge da parede à direita . Determine a condição sobre μ 2 que lhe permitiria fazer

6/2) O bloco de 50k g está em repouso sobre a superfície horizontal e uma força P = 200N , cuja direção pode ser variada , é aplicada ao bloco . (a) Calcule o coeficiente de atrito estático μ s , entr

6/8) A força P é aplicada ao bloco A de 200k g , que está apoiado em cima do caixote de 100k g . O sistema está em repouso quando P é inicialmente aplicada . Determine o que acontece acada corpo se (a

6/24) Determine a faixa das massas m para o qual o bloco de 100k g está em equilíbrio . Todas as polias e roldanas têm atrito desprezível .