Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 49

A seção transversal de uma viga extrudada é uma seção quadrada vazada de lado a = 75   m m e espessura t = 6,35   m m . Para uma força cortante vertical 65   k N , determinar a máxima tensão de cisalhamento na viga e esboçar o fluxo de cisalhamento na seção transversal.

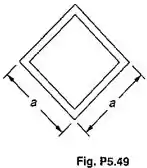
Passo 1

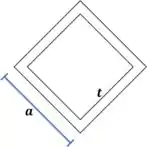
Pra começar vamos calcular o momento de inércia! Pra isso, vamos calcular o momento de inércia da região laranja em relação ao centro da figura.

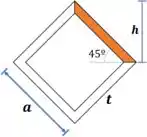
Podemos calcular o momento de inércia da região laranja considerando que é uma barra com momento de inércia na ponta:

I l a r a n j a = 1 3 A ⋅ h 2 I l a r a n j a = 1 3 a ⋅ t ⋅ a ⋅ sen ⁡ 45 2   I l a r a n j a = 1 6 a 3 t

E agora, o momento de inercia total é quatro vezes o valor da região laranja:

I = 4 I 1 = 2 3 a 3 t

Passo 2

O momento estático pode ser feito da mesma forma! Calcuamos o momento estático da região laranja:

Q l a r a n j a = a ⋅ t ⋅ h 2 Q l a r a n j a = a ⋅ t ⋅ a ⋅ sen ⁡ 45 º 2   Q l a r a n j a = 2 4 a 2 ⋅ t

E o momento estático máximo é o dobro do momento estático laranja

Q m a x = 2 Q l a r a n j a Q m a x = 2 ⋅ 2 4 a 2 ⋅ t  

Q m a x = 2 2 a 2 ⋅ t

Passo 3

Show!

Agora é só calcular a tensão no ponto:

τ = V Q m a x I ⋅ t m a x

Nesse caso a espessura da região é t m a x = 2 t

τ = V ⋅ 2 2 a 2 ⋅ t 2 3 a 3 t ⋅ 2 t τ = 3 2 8 V a t

E aplicamos os valores: τ = 3 2 8 65   k N 75   m m ⋅ 6,35   m m

Logo:

τ = 72,38   M P a

Resposta

τ = 72,38   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma correia fina é enrolada em torno de uma barra maciça de raio c = 20 mm, como mostrado. Sabendo-se que l = 100 mm e F = 5 kN, determinar as tensões, normal e de cisalhamento, no (a) ponto H; (b) po
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (a) a maior tensão normal.
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (c) a maior tensão de cisalhamento.
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (a) a maior tensão normal.
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (c) a maior tensão de cisalhamento.