Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 46a

Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensão de cisalhamento na viga. Esboçar também o fluxo de cisalhamento na seção transversal.

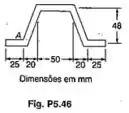
Passo 1

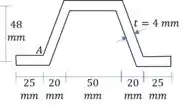
Da uma olhadinha na figura. Pode não parecer, mas o centroide dela é bem no meio. Note que a região inclinada não modifica a altura do centroide. E as abas na parte de baixo, tem o mesmo tamanho da barra superior.

Em outras palavras, podemos separar a figura da seguinte maneira:

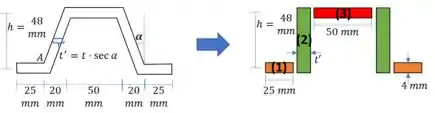
Note que a base da região inclinada é diferente da espessura.

tan ⁡ α = 20 48 ⇒ α = 22,62 º

t ' = t ⋅ sec ⁡ α = 4 ⋅ sec ⁡ 22,62 º ⇒ t = 4,33   m m

Com isso, podemos calcular o momento de inércia:

I = 2 I 1 + 2 I 2 + I 3

I = 2 ⋅ b 1 ⋅ t 3 12 + b 1 t ⋅ h 2 + 2 ⋅ t ' ⋅ h 3 12 + b 3 ⋅ t 3 12 + b 3 t ⋅ h 2

I = 2 ⋅ 25 ⋅ 4 3 12 + 25 ⋅ 4 ⋅ 48 2 + 2 ⋅ 4,33 ⋅ 48 3 12 + 50 ⋅ 4 3 12 + 50 ⋅ 4 ⋅ 48 2

I = 310,74 ⋅ 10 3   m m 4

Passo 2

Show! Agora que já temos o momento de inércia, precisamos calcular o momento estático!

Como a gente quer apenas o cisalhamento em A, então vamos calcular apenas o momento estático da região laranja!

Q A = 25 ⋅ 4 ⋅ 24

Q A = 2400   m m 3

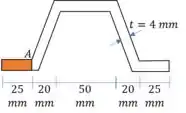
Passo 3

Agora é só aplicar a equação da tensão de cisalhamento:

τ A = V Q A I t

Aplica os valores:

τ A = 12   k N ⋅ 2400   m m 3 310,74 ⋅ 10 3   m m 4 ⋅ 4   m m

E prontinho:

τ A = 23,17   M P a

Resposta

τ A = 23,17   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga em balanço AB tem uma seção transversal retangular de 90 x 200 mm. Determinar: (a) o valor da força axial Q para que a tensão normal no ponto c seja -5,5 MPa; (b) as correspondentes tensões, no
A viga em balanço AB tem uma seção transversal retangular de 90 x 200 mm. Sabendo-se que a intensidade da força axial Q é 35,5 kN, determinar as tensões, normal e de cisalhamento, nos três pontos indi
Várias forças são aplicadas ao tubo mostrado. Sabendo-se que o tubo tem diâmetro, interno e externo, de 40 mm e de 48 mm, respectivamente, determinar as tensões normal e de cisalhamento no: (a) ponto
Uma correia fina é enrolada em torno de uma barra maciça de raio c, como mostrado. Sabendo-se que uma força vertical F é aplicada na correia, determinar em termos de F, c e l, as tensões, normal e de
Uma mola é feita de um arame circular de raio c, formando uma hélice de raio R. Determinar a máxima tensão de cisalhamento produzida pelas forças P e P’, iguais e opostas. (Sugestão: Determinar inicia