Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 60
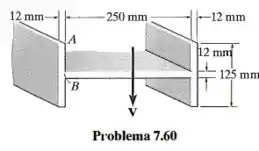
A viga suporta um cisalhamento vertical . Determine a força resultante desenvolvida no segmento AB.
Passo 1
Dados da questão:
A questão pede a força sobre o segmento
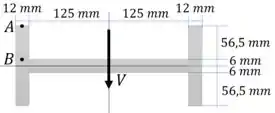
Estratégia de resolução: Como a figura é simétrica, não é preciso calcular o centroide. Vamos calcular o momento de inércia da seção e depois o momento estático do segmento AB.
Para encontrar a força sobre uma aba, será preciso integrar o fluxo de cisalhamento sobre a aba. Então, quais partes da equação serão integradas?
Bem, a força de cisalhamento já nos foi dada pela questão e é constante! O momento de inércia corresponde a figura como um todo, então também é constante! Já o momento estático varia de acordo com o ponto que queremos calcular, então ele não é constante!
Então, depois de calcular o momento de inércia, vamos desenvolver uma função que represente o momento estático na nossa aba.
Por fim, integraremos a equação do momento estático.
Passo 2
Passo 3
A figura abaixo mostra como o Momento Estático cresce. Ele inicia em uma ponta e vai seguindo rumo à linha do centroide. Para que todos os valores estejam relacionados com o centroide, imaginamos um eixo que parte da linha neutra até a base da região do momento estático.
Note que como todas as medidas estão em milímetros, os valores para também serão em milímetros
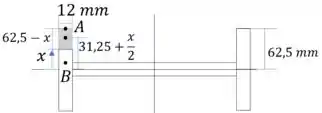
Observe também que da forma como estamos considerando o Momento Estático, esta formula só é válida para a aba , com . O nosso começa na linha centroide, mas o nosso limite de integração não chega até a linha do centroide
Um erro comum nesta questão é considerar os limites errados. Perceba que o ponto NÃO está sobre a linha do centroide, mas acima dela.
Passo 4
Agora basta usarmos a definição
Substituindo a fórmula do momento estático:
Como já discutido, os limites de são: .
Efetuando a integração:
Substituindo os valores os valores que temos: