Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 69

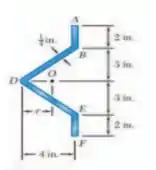
Determine a localização do centro de cisalhamento O de uma viga de parede fina uniforme espessura tendo a seção transversal mostrada.

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine a localização do centro de cisalhamento. Começamos localizando o eixo neutro e calculando o momento de inércia. Considere o esboço abaixo :D

Vamos determinar a área e inércia das seções deste elemento vem comigo :D

L D B = 4 2 + 3 2 = 5   i n   A D B = L D B τ = 5 1 4 = 1,25   i n 2

Seção DB:

I D B = 1 3 A A B h 2 = 1 3 1,25 3 2 = 3,75   i n 4

Seção AB:

I A B = 1 12 1 4 2 3 + 1 4 2 4 2 = 8,1667     i n 4

Para a inércia total temos:

I = 2 3,75 + 2 8,1667 =   23,833   i n 4

Passo 2

Seção AB temos:

A = 1 4 5 - y i n 2

y - = 1 2 5 + y i n

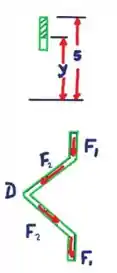
Aplicando abaixo:

Q = A y - = 1 8 5 - y 5 + y = 1 8 25 - y 2

Agora podemos determinar a tensão de cisalhamento:

τ = V Q I t = V 25 - y 2 8 23,833 0,25 = V 25 - y 2 47,667

F 1 = ∫ τ d A = ∫ 3 5 V 25 - y 2 47,667 ∙ 1 4 d y = V 190,667 25 y - 1 3 y 3 3 5

= V 190,667 25 5 - 1 3 5 3 - 5 3 + 1 3 3 3 = 0,0909 W

Calculando o momento em D temos:

+ ↶ M D = + ↶ M D : - V e = - 2 F 1 4 = - 0,7273 V

e = 0,727   i n

Resposta

0 , 727   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização do centro de cisalhamento O de uma viga de paredes finas de espessuras uniforme com a seção transversal mostrada.
Considere a viga em balanço AB discutida na Seção 6.5 e a parte ACKJ da viga que está localizada à esquerda da seção transversal CC´ e acima do plano horizontal JK, em que K é um ponto a uma distância
Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.
Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.
A viga em balanço AB, consistindo na metade de um tubo de paredes finas com raio médio de 31,8mm e espessura de parede de 9,53mm, está submetida a uma força vertical de 2224 kN. Sabendo que a linha de