Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 63

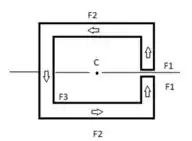
Determine a localização do centro de cisalhamento O de uma viga de paredes finas de espessuras uniforme com a seção transversal mostrada.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo: , começaremos determinando a inércia dividindo em regiões AB e BD , vem comigo :D

I A B = I F G = 1 3 t a 3           I D B = I C P = 2 a t a 3 + 1 12 a t t 3 ≈ 2 t a ³

I D E = 1 12 t 2 a 3 = 2 3 t a 3             I = Σ I = 16 3 t a ³

Passo 2

Agora vamos para seção: AB:

A = t y               y - = y 2             Q = 1 2 t y 2

τ = V Q I t = V ∙ 1 2 t y ² 16 3 t a ³ t = 3 V y 2 32 a 3 t

F 1 = ∫ τ d A = ∫ 0 a τ t   d y = 3 V 32 a 3 ∫ 0 a y ² d t = 1 32 V

Passo 3

Agora vamos para seção: BD:

Q = Q B + t x a = 1 2 t a 2 + t a x

τ = V Q I t = V t 16 3 a ³ t   1 2 a 2 + a x = 3 32 V a 2 a + 2 x

Para a força temos:

F 2 = ∫ τ d A = ∫ 0 2 a 3 V 32 a 3 a + 2 x d x = 3 V 32 a 3 a x + x ² 2 a 0 = 3 V 32 a 3 2 a ² + 4 a ² = 9 16 V

Calculando o momento temos:

+ ↺ Σ M H = + ↺ Σ M H :

V e = 2 a 2 F 1 + ( 2 a ) ( F 2 )

= 1 8 V a + 9 8 V a = 5 4 V a

e = 5 4 a = 1,250 a

Resposta

e = 5 4 a = 1,250 a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a distribuição de tensões de cisalhamento ao longo da linha D ' B ' na aba horizontal da cantoneira para o carregamento mostrado. Os eixos x ' e y ' são eixos principais da seção transversal
Para a cantoneira e o carregamento do Problema 6.81, determine a distribuição de tensões de cisalhamento ao longo da linha D ' A ' na aba vertical
Três pranchas são pregadas juntas de modo a formar a viga mostrada, a qual está submetida a uma força cortante vertical. Sabendo que o espaçamento entre os pregos é s = 75m m e a força cortante admiss
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto