Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 75

Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.

Passo 1

Galerinha, o enunciado pede que a gente determine a localização do centro de cisalhamento O da seção transversal. Vamos esboçar o diagrama de corpo livre, vem comigo :D

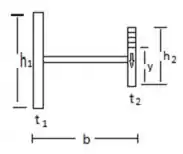
Consideramos a inércia abaixo :D

I = 1 12 t 1   h 1 3 + 1 12 t 2   h 2 3

No Flange direito temos:

A = 1 2 h 2 - y t 2

y - = 1 2 1 2 h 2 - y t 2

Q = A y -

= 1 2 1 2 h 2 - y 1 2 h 2 + y t 2 = 1 2 1 4 h 2 2 - y ² t 2

Passo 2

Então gurizada vamos considerar a tensão de cisalhamento abaixo

τ = V Q I t 2 = V 2 t 2 1 4 h 2 2 - y ² t 2

E a força é dada por:

F 2 = ∫ τ   d A = ∫ - h 2 / 2 h 2 / 2 V t 2 2 I t 2   1 4 h 2 2 - y ² t 2   d y = V t 2 2 I 1 4 h 2 2 y - y 3 3   h 2 / 2 h 2 / 2

= V t 2 2 I   1 4 h 2 2 h 2 2 - 1 3 h 2 2 3 + 1 4 h 2 2 h 2 2 - 1 3 h 2 2 3 = V t 2   h 2 3 12 I = V t 2   h 2 3 t 1   h 1 3 + t 2   h 2 3  

Passo 3

Então determinaremos o somatório do momento para obtermos a reação ;), consideramos o esboço abaixo :D

+ ↺ M H = + ↺ M H :                 - V e = - F 2 b = - V   t 2   h 2 3 b t 1   h 1 3 + t 2   h 2 3

e = t 2   h 2 3 b t 1   h 1 3 + t 2   h 2 3 = 0,75 6 3 8 0,75 8 3 + 0,75 6 3 = 2,37   i n .

Resposta

e = 2,37   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Se a altura h = 40 mm, determine o momento máximo que pode ser aplicado à viga se a tensão de flexão admissível para o alum
A viga composta é feita de alumínio 6061-T6 (A) e latão vermelho C83400 (B). Determine a dimensão h da tira de latão de modo que o eixo neutro da viga esteja localizado na costura dos dois metais. Qua
A viga em U de aço é usada para reforçar a viga de madeira. Determine a tensão máxima no aço e na madeira se a viga for submetida a um momento M = 1,2 kN.m. Eaço = 200 GPa, Emad = 12 GPa.
As partes superior e inferior da viga de madeira são reforçadas com tiras de aço, como mostra a figura. Determine a tensão de flexão máxima desenvolvida na madeira e no aço se a viga for submetida a u
O centro e os lados da viga de abeto Douglas são reforçados com tiras de aço A-36. Determine a tensão máxima desenvolvida na madeira e no aço se a viga for submetida a um momento fletor Mz = 10 kN.m.