Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 85

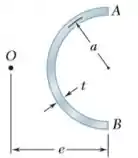
A viga em balanço AB, consistindo na metade de um tubo de paredes finas com raio médio de 31,8mm e espessura de parede de 9,53mm, está submetida a uma força vertical de 2224 kN. Sabendo que a linha de ação da força passa pelo centroide C da seção transversal da viga, determine (a) o sistema equivalente de força e momento do centro de cisalhamento da seção transversal e (b) a tensão de cisalhamento máxima da viga.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

I = π 2 a 3 t                         Q = a ² t sin ⁡ θ

e = 4 π a                               Q m a x = a ² t

Para uma seção de meio tubo, a distância do centro do semicírculo ao centroide é

x - = 2 π a

Em cada seção da viga, a força de cisalhamento V é igual a P. Sua linha de ação passa pelo centroide C. O seu momento sobre o centro de cisalhamento O é

d = e - x - = 4 π a - 2 π a = 2 π a

Passo 2

  1. Sistema de força-par equivalente em O, considere o esboço abaixo:

V = P                                                                 M O = V d = 2 π P a

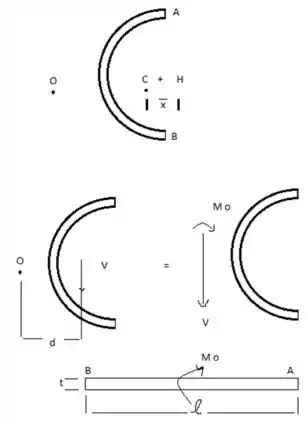
Data: P = 500 lb a=1,25 in.

V= 500 lb

  M O = 2 π ( 500 ) ( 1,25 ) = 398   l b ∙ i n .

Passo 3

(b) Tensão de cisalhamento.

(1) Devido a V:

τ V = V Q m a x I t

τ V = ( P ) ( a 2 t ) π 2   a 2 t ( t ) 2 P π a t = 2 500 π 1,25 0,375 = 679 p s i

(2) Devido ao torque   M O :

Para uma longa seção retangular de comprimento l e largura t , a tensão de cisalhamento devido ao torque   M O é

τ M = M O c 1 l t ²                         o n d e                     c 1 = 1 3 1 - 0,630 t l

Data:

l = π a = π 1,25 = 3,927 i n .             t = 0,375 i n .               c 1 = 0,3132 8

τ M = 397,9 ( 0,31328 ) ( 3,927 ) ( 0,375 ) ² = 2300   p s i

Por superposição,

τ + τ V + τ M = 679   p s i + 2300 p s i

τ = 298 0   p s i

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de (a) que é   M O = 398   l b ∙ i n ; e a resposta de (b) é: τ = 2980   p s i .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força de compressão máxima que a braçadeira de mola pode exercer sobre as chapas se a tensão de flexão admissível para a braçadeira for σadm = 4 MPa.
Para a cantoneira e o carregamento do Problema Resolvido 6,6 verifique se ∫ q dz =0 ao longo da aba horizontal da cantoneira d ∫ qd y = P ao de sua aba vertical.
Determine a localização do centro do centro de cisalhamento O de uma viga de paredes finas de espessura uniforme com o seção transversal mostrada.
Determine a localização do centro do centro de cisalhamento O de uma viga de paredes finas de espessura uniforme com o seção transversal mostrada.
Determine a localização do centro do centro de cisalhamento O de uma viga de paredes finas de espessura uniforme com o seção transversal mostrada.