Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 76

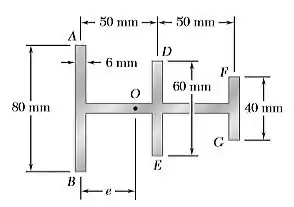
Uma viga de paredes finas tem a seção transversal mostrada. Determine a localização do centro de cisalhamento O da seção transversal.

Passo 1

Galerinha, tudo belezinha…? O enunciado pede que a gente determine a localização do centro de cisalhamento O da seção transversal. Considere o esboço abaixo ;)

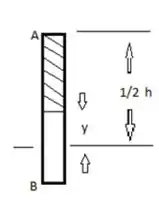
Vamos considera que:

h 1 = A B - = h ,                 h 2 = D E - ,                     h 3 = F G -

Sendo a inércia:

I = 1 12 t   ( h 1 3 + h 2 3 + h 3 3 )

Passo 2

Na parte AB temos que considerar o esboço abaixo ;)

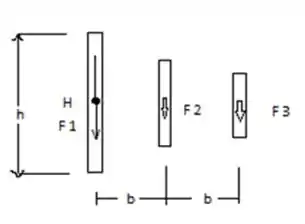
Temos que a área é dada por:

A = 1 2 h 1 - y   t

y - = 1 2 1 2 h 1 + y  

Onde:

Q = A y - = 1 2 t 1 2 h 1 - y   1 2 h 1 + y     = 1 2 t 1 4 h 1 2 - y ²  

A tensão de cisalhamento é dada por:

τ = V Q I t = V 2 I 1 4 h 1 2 - y ²

E a força é dada em relação a tensão acima ;)

F 1 = ∫ τ   d A = ∫ - 1 2 h 1 1 2 h 1 V 2 I   1 4 h 1 2 - y ² t   d y = V 2 I 1 4 h 1 2 - y 3 3 1 2 h 1 - 1 2 h 1

= V t I 1 4 h 1 2 1 2 h 1 - 1 3   h 1 2 3 = V t h 1 3 12 I = h 1 3 V h 1 3 + h 2 3 + h 3 3

Passo 3

Da mesma forma, para parte DE,

F 2 = h 2 3 V h 1 3 + h 2 3 + h 3 3

E para a parte FG,

F 3 = h 3 3 V h 1 3 + h 2 3 + h 3 3

O somatório do momento é dada por:

+ ↺ M H = + ↺ M H :       V e = b F 2 + 2 b F 3 =   b h 2 3 + b h 3 3 h 1 3 + h 2 3 + h 3 3

e = h 2 3 + 2 h 3 3 h 1 3 + h 2 3 + h 3 3

  b = 60 3 + 2 40 3 80 3 + 60 3 + 40 3 ( 50 )

e = 21,7 m

Resposta

  21,7 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os lados da viga de abeto Douglas são reforçados com tiras de aço A-36. Determine a tensão máxima desenvolvida na madeira e no aço se a viga for submetida a um momento fletor Mz = 4 kN.m. Faça um rasc
Determine a carga uniforme distribuída máxima w0 que pode ser suportada pela viga de concreto armado se a tensão de tração admissível para o aço for (σaço)adm = 200 MPa e a tensão de compressão admiss
A viga de concreto armado é feita com duas hastes de reforço de aço. Se a tensão de tração admissível para o aço for (σaço)adm = 280 MPa e a tensão de compressão admissível apara o concreto for (σconc
Determine o maior valor das forças aplicadas P se a tensão de flexão admissível for (σadm)c = 50 MPa sob compressão e (σadm)t = 120 MPa sob tração.
A braçadeira circular de mola produz uma força de compressão de 3 N sobre as chapas. Determine a tensão de flexão máxima produzida na mola A. A mola tem seção transversal retangular, como mostra a fig