Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 84

Determine e localize a resultante  R  das duas forças e do momento atuando na viga em I .

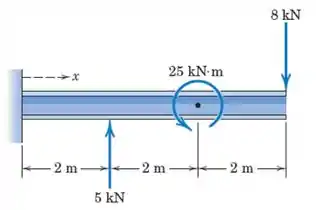
Passo 1

E aí meus queridxs, tudo bom com vocês? Espero que sim. Vamos começar nosso problema, fazendo a soma vetorial das nossas duas forças que será dada por

R → = - 8 ⋅ 10 3   j ^ + 5 ⋅ 10 3 j ^ =   - 3 ⋅ 10 3 j ^

Agora, vamos calcular o momento total do sistema em relação ao ponto onde temos a viga presa na parede. Dessa forma, obtemos

M = 5 ⋅ 10 3 ⋅ 2 + 25 ⋅ 10 3 - 8 ⋅ 10 3 ⋅ 6

O que resulta em

M = - 13 ⋅ 10 3   N ⋅ m

Lembrando que o sinal de negativo indica pra gente que essas forças favorecem uma rotação no sentido horário.

Passo 2

Pois bem, se queremos que a força R → produza o mesmo momento, M , que tínhamos inicialmente, precisamos escolher o ponto de aplicação da força de forma que

M = R → ⋅ x

13 ⋅ 10 3 = 3 ⋅ 10 3 ⋅ x → x = 13 3 ≈ 4,33 m

Além disso, teremos que R → aponta de cima para baixo, favorecendo uma rotação no sentido horário o que está completamente de acordo com o fato do nosso momento ter dado sinal negativo. Pronto, tá resolvido nosso problema.

Resposta

R → = - 13   k N ,   a p l i c a d a   e m   x = 4,33 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força F de 1800 N é aplicada à extremidade da viga em H. Expresse F como um vetor, usando os vetores unitários i e j.
A linha de ação da força F de 9,6k N passa pelos pontos A e B , como mostrado na figura. Determine os componentes escalares x e y de F .
Duas forças são aplicadas ao suporte de construção, como mostrado. Determine o ângulo θ que faz com que a resultante das duas forças seja vertical. Determine o módulo R da resultante.
Em que circunstâncias um sistema de forças aplicado a um corpo tem a tendência de provocar apenas translação? E, em provocar apenas rotação?
Por que, ao caminhar, o pé humano se comporta como uma alavanca inter-resistente? E por que, em uma mordida, o maxilar se comporta como uma alavanca interpotente?