Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 68

O sistema força-binário em  A  é substituído por uma força equivalente única no ponto  B  na aresta vertical (ou sua extensão) da placa triangular. Determine a distância  d  entre  A   e   B .

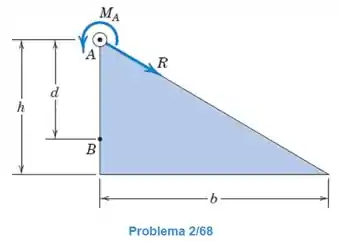
Passo 1

E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?

Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Pois bem, primeiramente vamos escrever o vetor unitário na direção e sentido de R que será dado por

n = b i - h j b 2 + h 2

Sendo assim, nosso vetor R pode ser escrito como

R = R ⋅ b i - h j b 2 + h 2

Passo 2

Então, nossa força equivalente em B deve gerar o mesmo momento em B . Dessa forma, escolhendo o ponto B (linha de ação da força R ) dado por

0 , - d

Teremos que nosso binário será dado por

M 0 = r × R = d   j × R ⋅ b i - h j b 2 + h 2

Manipulando nossa expressão vamos ter

M 0 = - R d b 2 + h 2 ⋅ j × b i - h j = R d b b 2 + h 2   k ^

Como nossa força em B deve gerar M a conseguimos encontrar a distância fazendo o módulo de M a e M 0 então teremos

M 0 = M a → R d b b 2 + h 2 = M a → R d b = M a b 2 + h 2 → d = M a b 2 + h 2 R ⋅ b

Pronto, tá resolvido nosso exercício. Falei que era rapidinho?

Resposta

d = M a b 2 + h 2 R ⋅ b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fieira é usada para abrir rosca em uma haste. Determine o modulo F das duas forças iguais exercidas sobre a haste de 6m m , para cada uma das quatro superfícies de corte, se forças iguais de 60N s
Reduza o sistema de carregamento dado a um sistema força-binário no ponto A . Em seguida, determine a distância x à direita do ponto A na qual atua a resultante das três forças.
Três binários são formados por três pares de forças iguais e opostas. Determine a resultante M dos três binários.
Uma força F atua ao longo da linha A B dentro da casca cilíndrica circular, à direita, como mostrado. As grandezas r ,h ,θ e F são conhecidas. Usando as coordenadas x ,yez mostradas, expresse F como u
A ação combinada das três forças sobre a base em O pode ser obtida estabelecendo sua resultante passando por O . Determine os módulos de R e do momento M associado.