Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 99
A figura mostra uma bomba manual de alta pressão usada para aumentar a pressão do óleo em uma linha hidráulica. Quando o manípulo estiver em equilíbrio em sob a ação de uma força , determine a pressão do óleo que atua no pistão de de diâmetro. (A pressão na parte superior do pistão é atmosférica.)
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a pressão do óleo que atua no pistão em de diâmetro igual a devido à força aplicada.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre da estrutura inteira:
Este problema nós vamos resolver analisando separadamente a barra . Entretanto, precisamos entender o sistema de forças que estão atuando. O ponto é comum a e , observe que ele deve ser paralelo a essa última para equilibrar com a reação na outra extremidade . Logo, podemos usar a barra para determinar a inclinação em relação à vertical da força em :
Passo 2
Show de bola! Agora que já temos a inclinação da reação em , podemos analisar a barra separadamente.
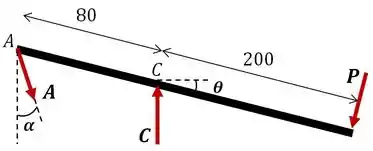
Uma vez que a estrutura está em equilíbrio, os membros separadamente também devem estar. Logo podemos fazer o equilíbrio de momentos em torno de para descobrir e, posteriormente, o equilíbrio de forças na direção vertical para determinar . Começando pelo momento em torno de , temos:
Passo 3
Finalmente, fazendo o equilíbrio de forças na direção vertical para a barra , encontramos a força no pistão :
Uma vez que a pressão é dada por:
Ufa! Essa já foi hein? Partiu pra próxima!
