Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 41
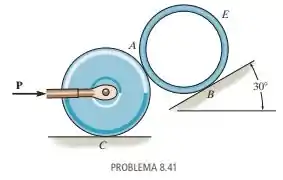
Determine a menor força necessária para empurrar o tubo para cima no aclive. A força atua paralelamente ao plano e os coeficientes de atrito estático nas superfícies de contato são , e . O rolete de e o tubo de possuem raios de
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Esta questão envolve muitas informações, vamos analisar os casos. Para que a força seja suficiente para empurrar ela deve ser suficiente para vencer o atrito que não deixa o ponto deslizar, deve ser sufiente para fazer com que o disco gire em relação ao tubo e ao mesmo tempo, deve ser suficiente para vencer o atrito no ponto
Primeiramente, para fazer o ponto deslizar:
A normal neste caso, vale o peso total:
Portanto:
Passo 2
Para o segundo caso, a força normal será dada pela componente do peso do tubo que é normal ao ponto logo:
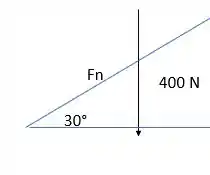
Logo, decompondo ela:
Logo, a força de atrito será:
A componente da força nesta direção deve superar a força de atrito:
Se ficar com dúvida de onde saiu a tangente de 30, desenho o triângulo com a força na horizontal e decomponha ela.
Passo 3
Agora, para o último caso, teremos a mesma situação acima, tirando o fato do coeficiente de atrito mudar, logo:
Para a situação inteira ser satisfeita, deve-se escolher o maior valor encontrado, que é: