Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 42

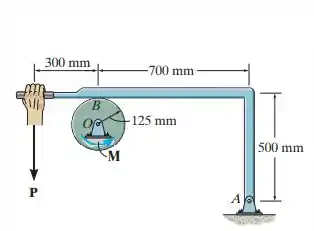
O coeficiente de atrito estático entre o tambor e a alavanca de freio é μ s = 0,4 . Sendo o momento M = 35   N ∙ m , determine a menor força P que precisa ser aplicada à alavanca a fim de impedir que o tambor gire. Além disso, determine as componentes horizontal e vertical da reação no pino O. Despreze o peso e a espessura da alavanca. O tambor tem massa de 25   k g .

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, devemos determinar o coeficiente de atrito máximo, para isso, vamos utilizar a segunda lei de Newton, temos:

F R = ∑ F

Para o eixo x , temos:

F R = ∑ F m ∙ a = - F a t + P cos ⁡ θ F R = N × μ s + 300 × 4 5 F R = 0,5 N + 240

Neste caso, a normal é igual ao peso, logo:

F 1 = g m u = 150 × 10 × 0,2 = 300   N

Passo 2

Agora, basta fazer o mesmo para o homem e o chão. A força de atrito entre o homem e o chão é dada por:

F 2 = 85 × 10 × 0,4 = 340   N

Logo, o homem conseguirá arrastar a caixa, pois o atrito entre seus sapatos e o chão é maior que o atrito da caixa com o chão.

Resposta

Sim, o homem conseguirá mover a caixa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

122- O coeficiente de atrito estático entre a braçadeira da furadeira de bancada e a coluna vertical vale 0.30 . Se o operador esquecer-se de prender a trava, a braçadeira e a mesa deslizarão para bai
143- Refira-se ao P r o b .6 / 142 onde a massa da barra uniforme vale 3k g , L = 2m e R = 1.2m . Conforme a força P é aumentada, o ângulo de equilíbrio θ também aumenta, desde que não ocorra deslizam
142- A barra esbelta uniforme de massa m e comprimento L está inicialmente em repouso, em uma posição horizontal centrada, sobre a superfície circular fixa de raio R = 0.6 L . Se uma força P normalmen
O bloco de 80 kg está colocado contra a mola em um plano com inclinação de 20° e é solto a partir do repouso. O coeficiente de atrito estático entre o bloco e o plano inclinado vale 0,25. ( b ) Calcul
Antes de correr, um corredor alonga as panturrilhas se inclinando contra uma parede, como mostrado na figura. Essa posição é atingida sem força vertical (atrito) entre suas mãos e a parede. Qual é o c