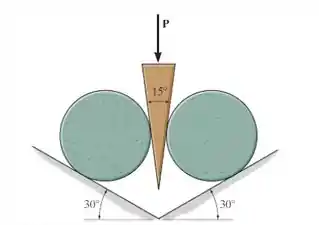
Determine a menor força vertical exigida para empurrar o calço entre os dois cilindros idênticos, cada um com peso . O coeficiente de atrito estático em todas as superfícies de contato é .

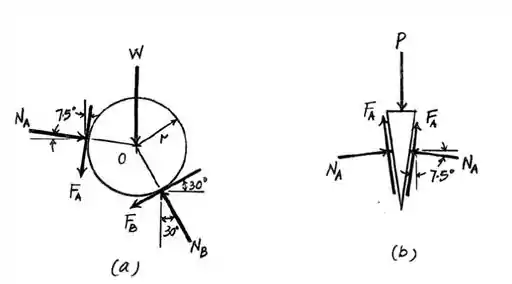
Galera, uma vez que o calço deve estar na iminência de se movimentar para baixo, as forças de fricção no calço deve estar direcionada para cima. Aqui temos duas possibilidades de movimento para o cilindro: a primeira o cilindro rola no plano inclinado (B) e escorrega no calço (A) ou a segunda, que o cilindro escorrega no calço (A) e escorrega no plano inclinado (B). Vamos assumir que a primeira situação ocorre e que .

Vamos analisar as forças no eixo na figura , referente ao cilindro. O somatório de forças, em um sistema em equilíbrio, deve ser igual a zero. Portanto, assumindo a direção para cima como positiva, temos:

Vamos analisar as forças no eixo na figura , referente ao cilindro. O somatório de forças, em um sistema em equilíbrio, deve ser igual a zero. Portanto, assumindo a direção para direita como positiva, temos:

Vamos calcular o momento em relação ao centro do cilindro. O somatório de momentos para um ponto, num sistema em equilíbrio é igual a zero. Logo, assumindo o sentido anti-horário como sentido positivo, temos:

Temos um sistema com três equações e três incógnitas. Vamos resolvê-lo!

Como , o escorregamento não vai ocorrer em B. Portanto, a afirmação feita no passo 2 é correta. Usando o resultado de , nós achamos:

Em relação ao diagrama , temos: