Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 47

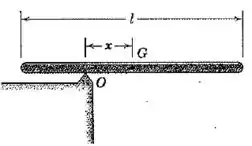
A barra uniforme esbelta é liberada a partir do repouso na posição horizontal mostrada. Determine o valor de para o qual aa aceleração angular é máxima, e determine a aceleração angular correspondente .

Passo 1

Queremos encontrar a aceleração angular da barra, então vamos precisar da seguinte fórmula:

Como calcular ? O momento de inércia da barra em relação ao centro de massa é seguinte:

E podemos calcular o momento de inércia em relação a um eixo que passa pelo ponto usando o teorema dos eixos paralelos:

Já que é a distância entre o centro de gravidade e o ponto onde a barra está apoiada.

Então nossa equação fica:

Passo 2

Agora precisamos escrever uma expressão para a soma dos momentos em relação ao ponto :

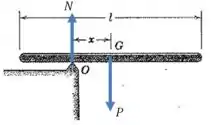
A única força que produz momento nesse caso é a força peso, que está a uma distância do ponto , então:

Então:

E isolando :

Nosso objetivo é encontrar o valor de que maximiza a aceleração angular, então temos que procurar os pontos de máximo dessa função , ou seja, os pontos que satisfazem a seguinte relação:

Para resolver essa derivada vamos precisar da regra do quociente:

Quando igualamos isso a zero, a expressão pode ser bastante simplificada, pois o denominador pode ser “cortado”:

Agora podemos dividir tudo por e reorganizar a equação:

Como as soluções negativas não fazem sentido nesse caso, a única solução é:

Passo 3

E podemos calcular a aceleração angular associada a esse valor de :

Substituindo :

Resposta

O valor que maximiza a aceleração angular é . Nesse caso, a aceleração angular é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A extremidade A da barra uniforme AB de 8 kg é ligada ao colar que pode deslizar sem atrito na barra vertical. A extremidade B da barra é ligada ao cabo vertical BC. Se a barra é liberada do repouso n

A barra uniforme BD de 300 mm e massa de 4 kg é ligada como mostra a figura à manivela AB e ao colar D de massa desprezível, que pode deslizar livremente ao longo de uma barra horizontal. Sabendo que

Resolva o Problema 16.127 quando θ = 90°.PROBLEMA 16.127 A barra uniforme BD de 300 mm e massa de 4 kg é ligada como mostra a figura à manivela AB e ao colar D de massa desprezível, que pode deslizar

A barra uniforme BD de 3 kg é ligada à manivela BD e ao colar de peso desprezível, que pode deslizar livremente ao longo de uma barra EF. Sabendo que, na posição mostrada na figura, a manivela BD gira

No Problema 16.129, determine a reação em A, sabendo que na posição mostrada na figura a manivela BD gira com uma velocidade angular de 15 rad/s e uma aceleração angular de 60 rad/s2, no sentido anti-