Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 227

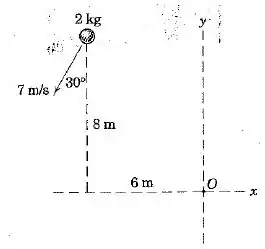
Determine o módulo H 0 da quantidade de movimento angular da esfera de 2   k g em torno do ponto O ( a ) usando a definição vetorial da quantidade de movimento angular e ( b ) usando uma abordagem escalar equivalente. O centro da esfera está localizado no plano x - y .

Passo 1

Bom galera, nesse exercício queremos determinar o valor de H 0 utilizando duas definições diferentes.

( a ) Pela definição vetorial de quantidade de movimento angular, temos

H O = r   x   m v

Substituindo os valores de acordo com o visto na figura, temos

H O = - 6 i + 8 j   x   2 7 - sin ⁡ 30 i - cos ⁡ 30 j

Ao cair nessa expressão, precisamos resolver o produto vetorial entre os vetores r e v . Ao resolver o produto vetorial, chegamos no seguinte valor

H O = 128,7   k g m 2 / s

Passo 2

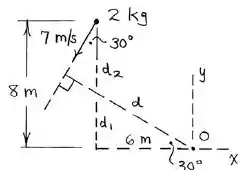
b Utilizando uma abordagem escalar, temos as seguintes distâncias

d 1 = 6 tan ⁡ 30 = 3,46

d 2 = 8 - d 1 = 4,54   m

Passo 3

Ao encontrar o valor de d 2 , podemos encontrar d pela seguinte relação

d = 6 cos ⁡ 30 + 4,54 sin ⁡ 30 = 9,2   m

Dessa forma, podemos utilizar a relação escalar para encontrar H O , chegando em

H O = m v d = 2 7 9,20 = 128,7 k g m 2 s

Resposta

H O = 128,7   k g m 2 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola de beisebol de 0,15k g tem uma velocidade de v = 30m / s , imediamente antes de ser atingida pelo taco. Após isso, ela desloca-se ao longo da trajetória mostrada, antes que o apanhador a pegue.
O bloco A , de 5k g , tem uma velocidade inicial de 5m / s ao descer por uma rampa lisa, após o que colide com o bloco estacionado B , de massa 8k g . Se os dois blocos acoplarem-se depois da colisão,
O pacote A , de 15k g , tem uma velocidade de 1,5m / s ao entrar na rampa lisa. Enquanto desliza rampa abaixo, atinge o pacote B , de 40k g , que está inicialmente em repouso. Se o coeficiente de rest
O canhão e o apoio, sem o projétil, têm uma massa de 250k g . Se um projétil de 20k g é disparado do canhão com uma velocidade vetorial de 400m / s , medida relativamente ao canhão, determine a veloci
Um vagão com massa de 15M g está se movendo a 1,5m / s sobre trilhos horizontais. Ao mesmo tempo, outro vagão, que tem massa de 12M g , está se movendo a 0,75m / s na direção oposta. Se os vagões enco