Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 246
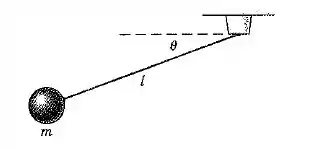
O pêndulo simples de massa e comprimento é liberado a partir do repouso em . Utilizando apenas o principio do impulso angular e quantidade de movimento, determine a expressão para em termos de e a velocidade do pêndulo em . Compare essa abordagem com uma solução pelo principio do trabalho-energia.
Passo 1
Bom galera, nesse exercício queremos encontrar uma expressão para em termos de e a velocidade do pêndulo em . Como a quantidade de movimento angular se conserva, temos que
Passo 2
Substituindo na expressão, temos
Isolando , ficamos com
Sabendo que , temos
Isolando , temos
Em ,
Passo 3
Pelo teorema,
Isolando , temos
Resposta
Exercícios de Livros Relacionados
O bloco de 5k g repousa sobre a superfície lisa. Sobre ele age uma força radial de 10N e uma força horizontal de 35N , sempre direcionada a 30 ° da tangente à trajetória como mostrado. Determine o tem
A bola de 1,5k g , localizada em A , é liberada do repouso e move-se para baixo sobre a trajetória curva. Se a bola exerce uma força normal de 25N sobre a trajetória quando alcança o ponto B , determi
O projétil de massa 3k g é disparado de um canhão a uma velocidade na boca do canhão v O = 500m / s . Determine a quantidade de movimento angular do projétil em relação ao ponto O no instante que ele
Inicialmente o bloco de 5k g está girando a uma velocidade escalar constante de 2m / s , em relação à trajetória circular centrada em O , sobre o plano horizontal liso. Se uma força tangencial constan
A partícula A de 2k g tem a velocidade mostrada. Determine sua quantidade de movimento angular H O em relação ao ponto O .