O pacote , de , tem uma velocidade de ao entrar na rampa lisa. Enquanto desliza rampa abaixo, atinge o pacote , de , que está inicialmente em repouso. Se o coeficiente de restituição entre e é , determine a velocidade de logo após o impacto.
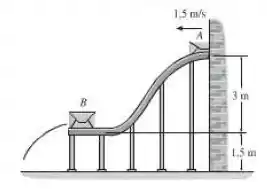
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de energia, temos:
Aplicando conservação de quantidade de movimento, temos:
O coeficiente de restituição é dado por:
Substituindo os valores, temos:
Relacionando as duas equações e resolvendo o sistema, temos: