Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas fundamentais - Ex. 12
O canhão e o apoio, sem o projétil, têm uma massa de . Se um projétil de é disparado do canhão com uma velocidade vetorial de , medida relativamente ao canhão, determine a velocidade do projétil, quando sai do cano do canhão. Despreze a resistência ao rolamento.
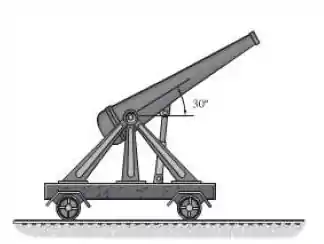
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando a conservação de movimento linear:
Substituindo os valores, temos:
Passo 2
Agora vamos estudar o movimento relativo. Temos:
Logo:
Do Passo 1, sabemos que , logo:
A magnitude da velocidade do projétil é dada por:
Resposta
Exercícios de Livros Relacionados
A viga uniforme AB de 100kg está perdurada inicialmente em repouso θ=00 quando a força constante P=300 N é aplicada ao cabo. Determine (a) a velocidade angular máxima atingida pela viga com o ângulo θ
Para um trem viaja a 160 km/h por uma curvatura horizontal com raio de 1,9 km, calcule o Ângulo de elevação β do trilho de modo que os passageiros sintam apenas uma força normal nos seus assentos e os
A viga I de aço deve ser transportada pelo carrinho suspenso ao qual está articulada em 0. Se o carrinho parte do repouso com θ ˙ = θ = 0 e recebe uma aceleração horizontal constante α = 2m/s², encont
Determine a massa da Terra sabendo que o raio médio da órbita da Lua em torno da Terra é de 382.250 km e que a Lua precisa de 27,32 dias para completar uma volta inteira em torno da Terra.
Um satélite é colocado em uma órbita circular em torno do planeta Saturno a uma altitude de 2100 milhas. O satélite descreve sua órbita com uma velocidade de 54,7x10³ mi / h. Sabendo que o raio da órb