Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 55
A área da seção transversal da escora de alumínio tem forma de cruz. Se ela for submetida ao momento , determine a tensão de flexão máxima na viga e faço o rascunho de uma vista tridimensional da distribuição de tensão que age em toda a seção transversal.
Passo 1
Fala galerinha bonita, tudo belezinha?
Saca só, nesse exercício aqui o enunciado nos informa que a área da seção transversal da escora de alumínio tem forma de cruz. Sabendo que ela está submetida ao momento , ele nos pede para determinar a tensão de flexão máxima na viga.
Primeiramente, vamos calcular o momento de inércia:
Como temos o momento, basta calcular a distância máxima da linha neutra, que será de
Logo:
Passo 2
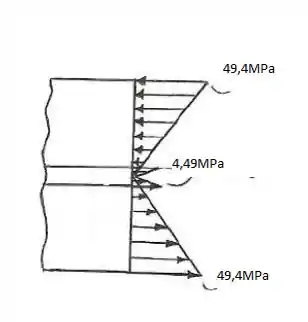
Podemos esboçar a distribuição de tensões:
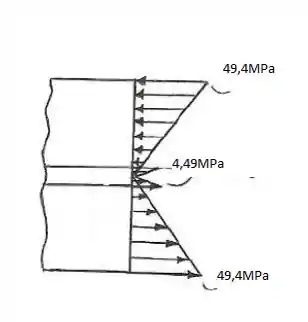
Resposta
Exercícios de Livros Relacionados
Se a viga ACB tiver seção transversal quadrada de 150m m por 150m m , determine a tensão de flexão máxima absoluta na viga.
Se a lança do guindaste ABC tiver seção transversal retangular com base de 60 mm, determine, com aproximação de múltiplos de 5 mm, a altura h exigida se a tensão de flexão admissível for σ = 170 MPa.
Determine a tensão de flexão máxima absoluta na viga. Cada segmento tem seção transversal retangular com base de 100m m e altura de 200m m .
Determine a tensão de flexão máxima absoluta no eixo de 40 mm de diâmetro que está sujeito às forças concentradas. Os mancais de luva em A e B suportam somente forças verticais.
Determine a tensão de flexão máxima absoluta no pino de 20m m de diâmetro.