Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 81

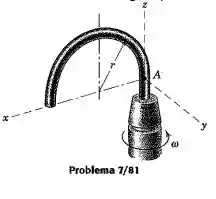
Determine o momento fletor M no ponto de tangência A na barra semicircular de raio r e massa m , enquanto a barra gira em torno do eixo tangente com uma velocidade angular constante e elevada ω . Despreze do momento m ⋅ g ⋅ r produzido pelo peso da barra.

Passo 1

Para resolvermos esse problema, usaremos as relações de momento fletor e precisaremos encontrar uma das componentes do tensor de inércia.

Passo 2

Temos que a força aplicada gera um torque na direção y . Assim, temos que nosso momento fletor será

∑ M y = - I x z ⋅ ω z 2

Para obtermos o momento de inércia precisamos calcular a seguinte integral:

I x z = ∫ x ⋅ z ⋅ d m = ∫ 0 π r + r ⋅ cos ⁡ θ ⋅ r ⋅ sin ⁡ θ ⋅ ρ ⋅ r ⋅ d θ

Onde ρ é a densidade por unidade de comprimento da barra. Resolvendo essa integral, chegamos que

I x z = 2 π ⋅ m ⋅ r 2

Substituindo no momento fletor, chegamos no resultado final de

∑ M y = - 2 π ⋅ m ⋅ r 2 ⋅ ω 2

Pegando o módulo dessa somatória, ficamos com

M = 2 π ⋅ m ⋅ r 2 ⋅ ω 2

Resposta

M = 2 π ⋅ m ⋅ r 2 ⋅ ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra uniforme tendo uma massa de 5 kg é suportada por um pino em A de um rolete que corre sobre um trilho horizontal. Se a barra está originalmente em repouso, e uma força horizontal F = 75N é ap
O navio tem uma massa de 2 ( 10 6 ) kg e cetro de gravidade em G. dois rebocadores de peso desprezível são usados para virá-lo. Se cada rebocador o empurra com uma força T =10 kN, determine a aceleraç
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração inicial da placa quando P = 100N for aplicada ao anel. A placa está originalmente em repouso.
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração angular inicial da placa quando P = 100 n for aplicada ao anel. A placa está originalmente em repouso.
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=200N for aplicada ao cabo, determine a aceleração de G e a aceleração angul