Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 170
Determine o momento da força em relação ao ponto .
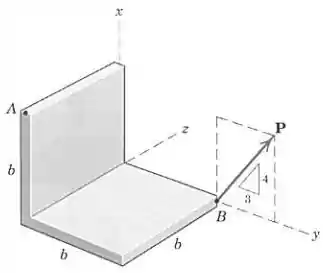
Passo 1
Vetorialmente, podemos escrever a força assim:
Além disso, o vetor posição que vai de até é:
Passo 2
Como a força é aplicada no ponto e queremos o momento em relação a , usamos a fórmula:
Resposta
Exercícios de Livros Relacionados
Determine o momento da força F C em relação a dobradiça da porta em A . Expresse o resultado como um vetor cartesiano.
Expresse o momento do binário atuando no encanamento na forma de um vetor cartesiano. Resolva o problema usando a Equação 4.13. Considere F = 25k →N .
Expresse o momento do binário atuando no encanamento na forma de um vetor cartesiano. Resolva o problema somando os momento de cada força em relação ao ponto O . Considere F = 25k →N .
Se o momento de binário atuando no encanamento possui uma intensidade de 400N ⋅ m , determine a intensidade F da força vertical aplicada em cada chave.
Substitua a força em A por uma força e momento de binário resultante equivalente no ponto P . Expresse o resultado na forma de vetor cartesiano.