Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 18
Determine o momento de inércia da manivela central em relação ao eixo . O material é aço, com um peso específico KN/m3.
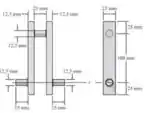
Passo 1
Pela geometria da figura, podemos calcular as massas de cada parte. Primeiro, vamos calcular a massa da conexão que liga os paralelepípedos. Com isso,
Agora iremos calcular a massa do paralelepípedo. Com isso,
Passo 2
Descobrimos as massas, então, agora, podemos calcular o momento de inércia com relação ao eixo . Então,
Resposta
Exercícios de Livros Relacionados
A roda tem uma massa de 15 kg e um raio de giração k G = 0,18m . Se os coeficientes de atrito cinético e estático entre a roda e o plano são μ s = 0,2 e μ k = 0,15 , determine a aceleração angular da
A roda tem uma massa de 15 kg e um raio de giração k G = 0,18m . Se os coeficientes de atrito cinético e estático entre a roda e o plano são μ s = 0,2 e μ k = 0,15 , determine o ângulo máximo θ do pla
Resolva o Problema 17.101 se μ s = 0,6 e μ k = 0,45 .
O disco semicircular de 10 kg está girando a ω = 4r a d / s no instante θ = 60 ° . Determine a força normal e de atrito que ele exerce sobre o solo em A nesse instante. Suponha que o disco não desliza
A bobina tem uma massa de 100 kg e um raio de giraçao k G = 0,3 m. se os coeficientes de atrito cinémetico e estático em A são μ k = 0,2 e μ s = 0,15 , respectivamente, determine a aceleração angular