Um carro de corrida move-se ao longo da pista circular com uma velocidade escalar de 16 m/s. Quando ele chega ao ponto A , ele aumenta sua velocidade escalar na razão de a t = ( 4 3 v 1 / 4 )m / s 2 , onde v é dado em m/s. Determine as intensidades da velocidade e aceleração do carro quando ele chega ao ponto B . Além disso, quanto tempo é necessário para ele se deslocar de A para B ?

v = 47,6m / s a = 11,8m / s 2 t = 10,11s

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 151

Um carro de corrida move-se ao longo da pista circular com uma velocidade escalar de 16 m/s. Quando ele chega ao ponto , ele aumenta sua velocidade escalar na razão de , onde é dado em m/s. Determine as intensidades da velocidade e aceleração do carro quando ele chega ao ponto . Além disso, quanto tempo é necessário para ele se deslocar de para ?

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade do carro: ;

Aceleração em : m/s2.

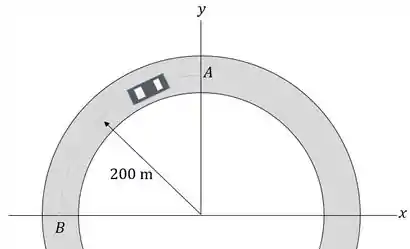
Raio de curvatura: .

Devemos determinar as intensidades da velocidade e aceleração do carro quando ele chega ao ponto e o tempo necessário para ele fazer esse trajeto .

Passo 2

Sabemos que a aceleração é igual a derivada temporal da velocidade

Para descobrirmos a equação da velocidade, devemos integrar a relação acima. Logo,

Passo 3

Sabemos que a velocidade é igual a derivada temporal do deslocamento

Para descobrirmos a equação do deslocamento, devemos integrar a relação acima. Logo,

Além disso, através da imagem fornecida, vemos que o deslocamento do carro é igual ao comprimento do arco que liga o ponto ao . O comprimento do arco é dado pela seguinte relação:

Onde está em radianos.

Logo, temos que

Igualando ambas as equações para , obtemos

Passo 4

A intensidade da velocidade é obtida ao substituir o valor de na equação de obtida no Passo 2.

Passo 5

Agora vamos encontrar a intensidade da aceleração:

Para isso, devemos definir os valores da aceleração normal e tangencial.

A aceleração normal é dada por:

Logo,

A aceleração tangencial é dada por:

Logo,

Substituindo esses valores em , obtemos

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro move-se ao longo de uma curva circular de raio r = 90 m. No instante mostrado, a sua taxa angular de rotação é θ ˙ = 0,4r a d / s , a qual está aumentando a uma taxa de θ ¨ = 0,2r a d / s 2 .

Uma partícula move-se ao longo de uma trajetória circular tendo um raio de 4 m, tal que sua posição como uma função do tempo é dada por θ = c o s 2 tr a d , onde t é dado em segundos. Determine a inte

Uma partícula move-se ao longo de um limaçon (ou caracol de Pascal) definido pela equação r = b - a c o s θ , onde a e b são constantes. Determine as componentes radiais e transversais da velocidade e

A posição de uma partícula é descrita por r = 300 e - 0,5 tm m e θ = 0,3 t 2r a d , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 1,5 s.

Uma partícula move-se ao longo de uma espiral de lituus definida pela equação r 2 θ = a 2 , onde a é uma constante. Determine as componentes radiais e transversais da velocidade e aceleração da partíc