Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 107

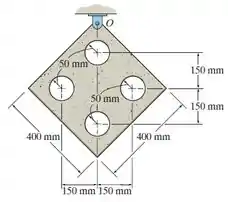
Determine o momento de inércia de massa da chapa fina em relação a um eixo perpendicular à página e que passa pelo ponto O . O material tem 20   k g / m 2 de massa por unidade de área.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos calcular o momento de inércia de massa da chapa em relação ao eixo perpendicular à página O .

Só que nós não temos nenhuma fórmula para a placa com furos. Temos apenas para a região circular como para a placa quadrada.

Então, o que temos que fazer é calcular o momento de inércia da placa e retirar deste valor os momentos de inércia das regiões circulares.

Então, vamos relembrar as fórmulas. Começando pela placa quadrada, temos:

I p l a c a = M a 2 + b 2 12

Sendo M a sua massa, a = b = 0,4   m . Já para a região circular, temos:

I c í r c u l o = m r 2 2

Sendo r = 0,0 5   m .

Bom, as relações acima são para o momento de inércia em relação ao eixo que passa pelo centro de massa. Mas o que queremos é o momento em relação ao eixo O . Por causa disto, vamos ter que trabalha com o teorema de eixos paralelos.

Só que nós só veremos este teorema depois, pois temos um problema maior antes: qual é a massa dos componentes??? Então, vamos calculá-los!

Passo 2

Vamos calcular a massa das regiões circulares e da placa. Aqui é jogo fácil. Basta lembrar que a massa é o produto da densidade pela área! Portanto, começando pela placa, temos:

M = ρ A p l a c a = ρ a 2

M = 20 ⋅ 0 , 4 2

M = 3,2   k g

Já para o círculo, temos:

m = ρ A c í r c u l o = ρ π r 2

m = 20 ⋅ π ⋅ 0,0 5 2

m = 0,157   k g

E assim terminamos de determinar a massa dos componentes!

Passo 3

Para que a gente consiga calcular o momento de inércia, vamos nos lembrar do teorema dos eixos paralelos. Ele nos diz que:

I = I G + m d 2

Sendo I G o momento de inércia que passa pelo centro de massa da peça, I o momento de inércia que queremos e d a distância entre os dois eixos.

Para a placa, a distância do centro de massa até o ponto O é d p l a c a = 0,283   m . Já para as regiões circulares, temos três distâncias diferentes: d 1 = 0,133   m , d 2 = 0,433   m e d 3 = 0,32   m (os dois círculos laterais).

Então, só nos resta calcularmos o momento de inércia. Portanto,

I O = I p l a c a + M d p l a c a 2 - I c í r c u l o + m d 1 2 - I c í r c u l o + m d 2 2 - 2 ⋅ I c í r c u l o + m d 3 2

I O = I p l a c a + M d p l a c a 2 - 4 I c í r c u l o - m d 1 2 + d 2 2 + 2 d 3 2

I O = 3,2 ⋅ 2 ⋅ 0,4 2 12 + 3,2 ⋅ 0,283 2 - 4 0,157 ⋅ 0,05 2 2 - 0,157 0,133 2 + 0,433 2 + 2 ⋅ 0,32 2

I O = 0,0 853 + 0,2563 - 0,000785 - 0,0644

I O = 0 , 276   k g ⋅ m 2

E assim finalizamos a questão!

Resposta

I O = 0,276   k g ⋅ m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os elementos finos possuem massa de 4k g / m . Determine o momento de inércia do conjunto em relação a um eixo perpendicular à página e que passa pelo ponto A .
Determine o momento de inércia do elipsoide em relação ao eixo x e expresse o resultado em termos da massa m do elipsoide. O material tem densidade constante ρ .
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m  do paraboloide. O materi
Resolva o Problema 10.78 usando o círculo de Mohr.
Resolva o Problema 10.80 usando o círculo de Mohr.