Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 65
A grua pode ser ajustada para qualquer ângulo e qualquer extensão . Para uma massa suspensa de , determine o momento desenvolvido em em função de e . Que valores de e desenvolvem o momento máximo possível em ? Calcule esse momento. Desconsidere o tamanho da polia em .
Passo 1
Tudo certinho aí pessoal? Vamos para mais um exercício.
Nesta questão, vamos desenvolver uma equação geral do momento para o sistema e depois aplicar os valores máximos do enunciado.
Como queremos descobrir o momento em , vamos fazer o somatório de momentos nesse ponto. Mas primeiro, é sempre importante fazer o diagrama de corpo livre do sistema.
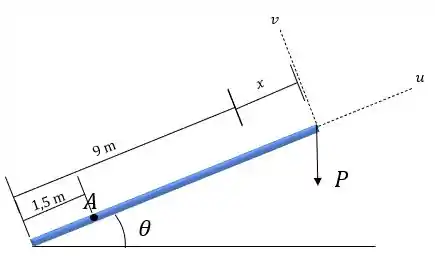
Decompondo , temos:
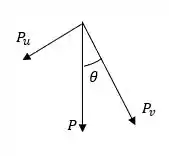
Portanto:
Sabendo que , temos que:
Agora é só armar o nosso somatório de momento.
A equação do momento em para o sistema será:
Passo 2
Agora que encontramos a equação, vamos aplicar os valores que irão geram um momento máximo.
Fazendo uma análise rápida e sabendo que , temos que o valor do momento será máximo quando e . Pois . Logo: