Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 93

Determine o momento de inércia I z do tronco de cone, que possui uma depressão cônica. O material tem densidade de 2000   k g / m 3 .

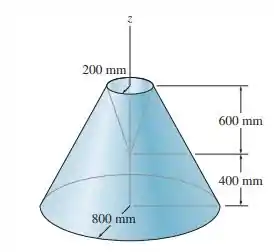
Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Este problema nos pede para determinarmos o momento de inercia I z para este tronco de cone. Primeiro, vamos dividir este tronco de cone em 3 cones. Fica assim:

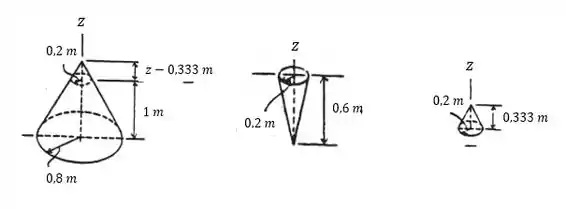
Em seguida, vamos utilizar a semelhança de triângulos, temos:

z 0,2 = z + 1 0,8 z = 0,333   m

Passo 2

Com isso, vamos determinar o momento de inercia de massa de cada um desses cones. Eles são dados por:

I z = 3 10   m r 2

Substituindo, temos:

I z = ∑ I z i = 3 10 π 3 0,8 2 1,333 200 0,8 2 - … - 3 10 π 3 0 , 2 2 , 333 200 0 , 2 2 - … - 3 10 π 3 0 , 2 2 0,6 200 0 , 2 2

Resolvendo, temos que I Z   vai ser:

I z = 34,2   k g ∙ m 2  

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I z = 34,2   k g ∙ m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da área da seção transversal em relação ao eixo x .
Determine a distância x - até o centroide C da área da seção transversal da viga; depois, ache o momento de inércia I - y ' em relação ao eixo y ' .
Determine y - , que localiza o eixo centroidal x ' da área da seção transversal da viga “ T ” , e depois calcule o momento de inércia em relação ao eixo x ' .
Determine a distância y - até o centroide C da área da seção transversal da viga; depois, ache o momento de inércia I - x em relação ao eixo x ' .
Determine o produto de inércia do área sombreada em relação aos eixos x e y .