Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 2i

Determine os momentos das forças representadas na próxima figura, em relação às origens dos sistemas cartesianos indicados

Passo 1

Para resolver essa questão, vamos relembrar a definição de momento da força. O momento de uma força F → = ( F X   , F Y   , F Z ) , é o produto vetorial dessa força pelo vetor r → = ( X , Y , Z ) . Para facilitar um pouco, basta lembrar que as componentes do momento da força são dadas por

M X = Y   F Z - Z   F Y

M Y = Z   F X - X   F Z

M Z = X   F Y - Y   F X

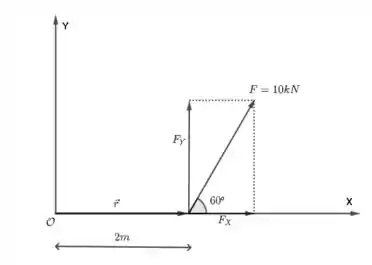
Então, temos que determinar qual é o vetor r → e decompor o vetor força nas direções x , y e z . O vetor r → é aquele que sai da origem e vai até o ponto de início do vetor força. Na figura acima, vemos que r → só tem componentes em x e magnitude igual a 2 m . Então

r → = ( 2 m , 0,0 )

Passo 2

Agora, vamos decompor a força F = 10   k N , em relação ao ponto ( 2,0 , 0 ) . Como a força faz 60   ° com o eixo x e está no plano x y , então F Z = 0 e as demais componentes são

F X   = F c o s   θ   = 10   k N c o s 60   ° = 10   k N ⋅ 0,5 = 5   k N    

F Y   = F   s e n     θ = 10   k N   s e n   60   ° = 10   k N ⋅ 0,866 = 8,66   k N   ≈ 8,7   k N

Passo 3

Agora que sabemos as componentes da força e do vetor r → , podemos substituir na fórmula do momento da força

M X = 0 - 0 ⋅   8,7   k N = 0

M Y = 0 ⋅ 5 k N - 0 = 0

M Z = 2 m ⋅   8,7   k N - 0 ⋅ 5   k N = 17 , 4   k N m

Logo, o momento da força só tem componentes na direção z . Esse resultado já é esperado, porque o momento da força é perpendicular a F → e r → , que nesse caso estão no plano x y .

Resposta

M 0 → = 17,4   k N m   k ^

Exercícios de Livros Relacionados

Determine a intensidade e o sentido direcional da força em A em relação ao ponto O .
Determine o momento produzido por cada força em relação ao ponto A.
O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em B para que essa força crie um momento máx
Determine o momento da força em relação ao ponto O.Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine o momento da força em relação ao ponto O.Fonte: Estática Mecânica para Engenharia – 14ª ed