Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 13ii

Com a condição de que as barras da figura abaixo estejam em equilíbrio, determine a intensidade das forças F → i

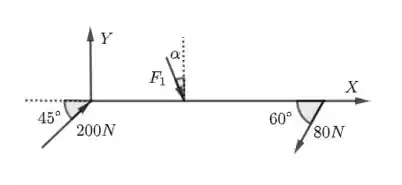
Passo 1

Nessa questão, as forças tem componentes tanto em x quanto em y . Logo, temos que utilizar as equações de equilíbrio ∑ F X = 0 e ∑ F Y = 0 . A força de 200   N tem componentes

F → 200 =   200   N   c o s 45 ° i ^ + 200   N   s e n   45 °   j ^ =   200   N   ⋅ 0,707 i ^ + 200   N ⋅ 0,707   j ^

= 141,4   N   i ^ + 141,4   N   j ^

A força de 80   N tem componentes

F → 80 =   80   N   c o s 60 ° i ^ + 80   N   s e n   60 °   j ^ =   80   N   ⋅ 0,5 i ^ + 80   N ⋅ 0,866   j ^ =   40 N   i ^ + 69,3 N   j ^

Por último, mas não menos importante, F → 1 tem componentes F → 1 =   F 1 s e n   α   i ^ - F 1   c o s   α   j ^ .

Passo 2

Agora vamos aplicar as equações de equilíbrio:

∑ F X = 141,4   N + 40   N + F 1   s e n   α = 0 ⇒ F 1   s e n   α = - 141,4   N - 40   N = - 181,4   N

∑ F Y = 141,4   N + 69,3   N - F 1   c o s   α = 0   ⇒ F 1   c o s   α = - 141,4   N - 69,3   N = 210,7   N

Assim, vemos que é necessário saber qual o ângulo α para poder determinar o módulo de F → 1 . Calma! Podemos dividir a primeira equação acima pela segunda e com isso obter uma expressão para o ângulo:

F 1   s e n   α F 1 c o s     α =   s e n   α   c o s   α = t a n   α = - 181,4   N - 210,7   N = 0,86   ⇒ α = a r c t a n   ( 0,86 )   = 40,7 °

Passo 3

Agora que sabemos que α = 40,7 ° , podemos utilizar o resultado da segunda equação de equilíbrio para determinar o módulo de F → 1 :

F 1 = 210,7   N c o s   47 ° = 210,7   N 0,758 ≈ 278   N

Resposta

F 1 = 278   N

Exercícios de Livros Relacionados

A treliça simples assimétrica é carregada conforme mostrado. Determine as reações em A e D . Despreze o peso da estrutura em comparação com as cargas aplicadas. É necessário ter conhecimento do tamanh
Uma força axial 700N é necessária para remover a polia de seu eixo. Que força F deve ser exercida na alça de cada uma das duas alavancas? O atrito nos pontos de contato B e E é suficiente para evitar
Um tubo P está sendo dobrado pelo dobrador de tubos, conforme mostrado. Se o cilindro hidráulico aplica uma força de magnitude F = 24k N ao tubo em C , determine a magnitude das reações do rolo em A e
Determine a magnitude P da força vertical necessária para levantar o carrinho de mão livre do solo no ponto B . O peso combinado do carrinho de mão e sua carga é 240l b com centro de gravidade em G .
Uma força axial de 35N em B é necessária para abrir o êmbolo com mola do bico de água. Determine a força necessária F aplicada à alça em A e a magnitude da reação do pino em O . Observe que o êmbolo p