Passo 1
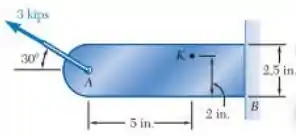
E ai gurizada tudo bem? O enunciado pede que a gente determine os planos principais e as tensões principais no ponto K, (b) a máxima tensão de cisalhamento no ponto K. Vamos determinar as forças ;)
Na seção contendo os pontos H e K,
Passo 2
Propriedades da seção. considerem o meu esboço abaixo :D
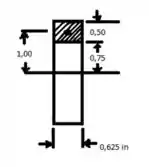
No ponto k,
Passo 3
Tensão no ponto K.
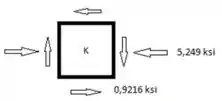
Passo 4
Círculo de Mohr’s
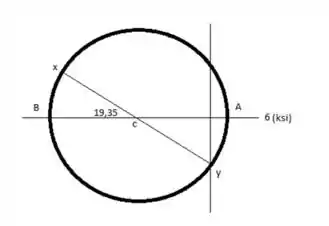
Passo 5