Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 51

Três forças são aplicadas à componente de máquina ABD mostrado na figura. Sabendo que a seção transversal contendo o ponto H é um retângulo de 20mmx40mm, determine as tensões principais e a tensão de cisalhamento máxima no ponto H

Passo 1

E ai gurizada tudo certo? O enunciado pede que a gente determine as tensões principais e a tensão de cisalhamento máxima no ponto H. Considere o esboço a seguir:

F x = - 3 k N ,   F y = - 0,5 k N ,   F z = - 2,5 k N

M x = 0 ,   M y = 0,150 2500 = 375 N ∙ m

M z = - 0,150 500 = - 75 N ∙ m

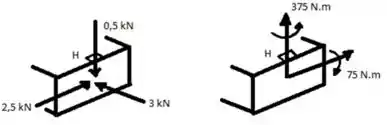
Passo 2

Agora temos que determinar a inércia antes começaremos pela área, vem comigo :D

A = 20 40 = 800 m 2 = 800 x 10 - 6 m 2

I z = 1 12 40 20 3 = 26,667 x 10 3 m m 4 = 26,667 x 10 - 9 m 4

σ H = P A - M z y I 2 = - 3000 800 x 10 - 6 - 75 10 x 10 - 3 26,667 x 10 - 9 = 24,375 M P a

τ H = 3 2 V z A = 3 2 ∙ 2500 800 x 10 - 6 = 4,6875 M P a

Passo 3

Usando círculo de Mohr

σ a v e = 1 2 σ H

= 12,1875 M P a

R = 24,375 2 2 + 4,6875 2

= 13,0579 M P a

σ a = σ a v e + R             σ = 25,2   M P a

σ b = σ a v e - R           σ b = - 0,87   M P a

t a n 2 θ p = 2 τ H σ H = 2 4,6875 24,375 = 0,3846

σ a = 10,5 ° ,   σ b = 100,5 °

τ M A X = R                               τ M A X = 13,06 M P a

Resposta

τ M A X = 13,06 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5 8 - i n .,determine a os planos principais e as tensões principais no ponto K, (b) a máxima tensão de cisalhamento no ponto K.
Forças são aplicadas nos pontos A e B do suporte em ferro fundido mostrado. Sabendo que o suporte tem um diâmetro de 0,8in., determine as tensões principais e a máxima tensão de cisalhamento no (a) po
Sabendo que o tubo estrutural mostrado tem parede de espessura constante de 6,35 mm, determine as tensões normal e de cisalhamento nos três pontos indicados.
Sabendo que o tubo estrutural mostrado tem parede de espessura constante de 6,35 mm, determine as tensões normal e de cisalhamento nos três pontos indicados.
Para o poste e o carregamento mostrados na figura, determine as tensões principais, os planos principais e a tensão de cisalhamento máxima no ponto H.