Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 52
(8.51) Três forças são aplicadas à componente de máquina ABD mostrado na figura. Sabendo que a seção transversal contendo o ponto H é um retângulo de 20mmx40mm, determine as tensões principais e a tensão de cisalhamento máxima no ponto H. 8.52: Resolva o problema 8.51, considerando que a intensidade da força de 2,5kN foi aumentada para 10kN
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine tensões principais e a tensão de cisalhamento máxima no ponto H. Considere o esboço abaixo
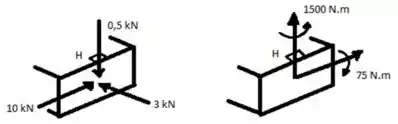
Passo 2
Agora temos que determinar a inercia considere nosso esboço ;)
A tensão de cisalhamento é dada por:
Temos que:
Resposta
Exercícios de Livros Relacionados
O anel cujas dimensões são mostradas na figura é colocado sobre uma membrana flexível bombeada com uma pressão p. Determine a mudança no raio interno do anel após a aplicação dessa pressão. O módulo d
O tubo de extremidade aberta feito de cloreto de polivinil tem diâmetro interno de 100 mm e espessura de 5 mm e transportar água corrente à pressão de 0,42 MPa. Se esse fluxo no interior do tubo for i
O barril está cheio de água até em cima. Determine a distância s entre o aro superior e o aro inferior de modo que a força de tração em cada aro seja a mesma. Determine também a força em cada aro. O b
A cinta de aço A-36 tem 50 mm de largura e está presa ao redor do cilindro rígido. Se os parafusos forem apertados de modo que a tração neles seja 2 kN, determine a tensão normal na cinta, a pressão e
A figura mostra duas alternativas para apoiar o cilindro de parede fina. Determine o estado de tensão na parede do cilindro para ambas as alternativas, se o pistão P provocar uma pressão interna de 0,