Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 47

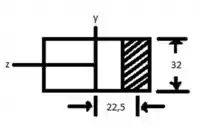
Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.). Primeiramente devemos calcular a área ;)

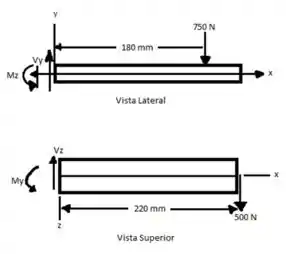
Agora devemos determinar a inércia, vem comigo :D

A = 60 32 = 1920 m m 2 = 1920 x 10 - 6 m 2

I z = 1 12 60 32 3 = 163,84 x 10 3 m m 3 = 163,84 x 10 - 9 m 4

I y = 1 12 32 60 3 = 579 x 10 3 m m 4 = 576 x 10 - 9 m 4

Passo 2

Na seção contendo os pontos a, b, e c,

P = 10 k N

V y = 750 N ,

V z = 500 N

Determinando os momentos em z e y temos:

M z = 180 x 10 - 3 750 = 135 N ∙ m

M y = 220 x 10 - 3 500 = 110 N ∙ m

T = 0

σ = P A + M z y I z - M y z I y

τ = V z Q I y t

Passo 3

  1. Ponto a: y = 16 m m ,       z = 0 ,   Q = A z - = 32 30 15 = 14,4 x 10 3 m m 3

    2. σ = 10 x 10 3 1920 x 10 - 6 + 135 16 x 10 - 3 163,84 x 10 - 9 - 0                                             σ = 18,39 M P a

    τ = ( 500 ) ( 14,4 x 10 - 6 576 x 10 - 9 32 x 10 - 3                                                                 τ = 0,391 M P a

    Passo 4

  2. Ponto b: y = 16 m m ,     z = - 15 m m ,     Q = A z - = 32 15 22,5 = 10,8 x 10 3 m m 3

    3. σ = 10 x 10 3 1920 x 10 - 6 + 135 16 x 10 - 3 163,84 x 10 - 9 - 110 - 15 x 10 - 3 576 x 10 - 9                 σ = 21,3 M P a

    τ = 500 10,8 x 10 - 6 576 x 10 - 9 32 x 10 - 3                                                                                                                                       τ = 0,293 M P a

    Passo 5

  3. Ponto C: y = 16 m m ,     z = - 30 m m ,     Q = 0

σ = 10 x 10 3 1920 x 10 - 6 + 135 16 x 10 - 3 163,84 x 10 - 9 - 110 - 30 x 10 - 6 576 x 10 - 9                  

σ = 24,1 M P a

τ = 0

Resposta

  1. σ = 18,39 M P a   e   τ = 0,391 M P a  
  2. σ = 21,3 M P a   e     τ = 0,293 M P a
  3. σ = 24,1 M P a   e   τ = 0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força de 6kip é aplicada ao elemento de máquina AB conforme mostrado. Sabendo que o elemento tem espessura uniforme igual a 0,8 in., determine as tensões normal e de cisalhamento no (a) ponto a, (
Sabendo que as hastes BC e DC têm diâmetros de 24mm e 36mm, respectivamente, determine a tensão de cisalhamento máxima em cada haste. Despreze os efeitos das hastes e das concentrações de tensão.
τ a d m = 55 M P a e considerando que são transmitidos 8 k W na engrenagem F e 12kW na engrenagem G, determine o menor diâmetro admissível para o eixo AB.
r. Determine a tensão de cisalhamento máxima produzida pelas duas forças iguais e opostas PeP ' . Sugestão: primeiramente, determine a força cortante V e o torque T em uma seção transversal.)
I = 100 m m e F = 5 k N , determine as tensões normal e de cisalhamento no a no ponto H , b ponto K.