Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 61

A viga está sujeita às duas cargas concentradas. Supondo que o alicerce exerça uma distribuição de carga linearmente variável em sua base, determine as intensidades de carga w1 e w2 para que haja equilíbrio em termos dos parâmetros mostrados.

Passo 1

Oi, tudo bem? Vamos analisar esta questão.

Para este sistema, quando submetemos as cargas e como representado na figura, teremos uma reação que equivale a uma distribuição de carga linearmente variável.

Observe o diagrama de corpo livre. Temos que:

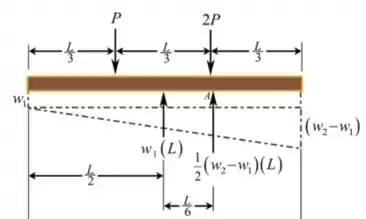
Como representado no diagrama, podemos dividir a distribuição de carga em duas, uma retangular e uma triangular. E teremos as forças equivalentes a elas.

Passo 2

Vamos fazer o somatório de momentos no ponto :

Fazendo agora o somatório das forças em , temos que:

Simplificando e resolvendo, teremos que:

Vamos para o próximo exercício?

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem fica em pé na ponta do trampolim que é sustentado por duas molas A e B, cada uma com rigidez k = 15 kN/m. Na posição mostrada, o trampolim é horizontal. Se o homem possui uma massa de 40 kg ,

Um instrumento de detecção submarina A está preso ao ponto médio de um cabo de 100 m, suspenso entre dois barcos distando 50 m entre si. Determine a profundidade h do instrumento, que tem massa despre

O centro de flutuação B do casco de um navio é o centroide do seu volume submerso. As seções transversais das áreas submersas A , ao longo da direção transversal do casco do rebocador mostrado, estão

Um cabo, com massa de 15 kg/m, está preso ao ponto A e passa sobre uma pequena polia B, situada sobre a mesma linha horizontal que A. Determine a deflexão h e o comprimento S do cabo entre A e B , se

Um determinado comprimento de um cabo de transmissão está suspenso das duas torres, como mostrado. O cabo tem uma massa de 20 kg por metro. Se a máxima força trativa admissível no cabo vale 75 kN, det