Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 59
Determine a distância para a posição da carga para que haja equilíbrio da haste lisa na posição , como mostra a figura. Desconsidere o peso da haste.
Passo 1
Vamos para mais um exercício?
Como o enunciado nos disse, queremos a distância que faz com que o equilíbrio seja mantido na posição .
A primeira coisa que devemos fazer é um diagrama de corpo livre do sistema para ver como as reações irão se comportar.
Temos o seguinte diagrama:
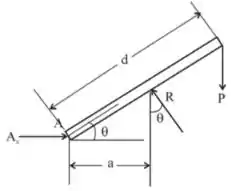
Você deve ter notado que não consideramos a reação em no ponto . Isso acontece por que devemos desconsiderar o peso da barra e já que ela está encostada, a reação .
Passo 2
Fazendo um somatório das forças em , temos que:
Podemos fazer o somatório de momentos no ponto também:
Substituindo , temos que:
Simplificando e resolvendo para , temos que:
Esta equação irá determinar a distância , do sistema da figura do enunciado, em que existe equilíbrio estático.
Consegui te ajudar? Responde Aí!