Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 60
A haste suporta um cilindro com massa de e tem um pino em sua extremidade . Se ela estiver sujeita a um momento de binário de , determine o ângulo para que haja equilíbrio. A mola tem um comprimento, quando não estendida, de , e uma rigidez .
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Aqui, queremos o ângulo que mantém o sistema estático.
Primeiro, vamos construir o diagrama de corpo livre. Temos que:
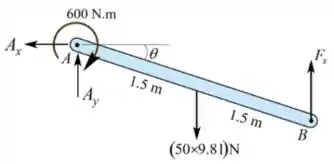
e são as reações no ponto . O termo é referente ao peso do cilindro e é a força de reação da mola.
Temos que:
Este termo indica o estiramento da mola após o peso ser adicionado ao sistema.
Passo 2
Vamos fazer o somatório de momentos no ponto :
Temos que:
E como , temos que:
Esta equação pode ser resolvida em um software de cálculo, como o EES.
O resultado será:
Consegui te ajudar? Responde Aí!