Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 118
Determine a projeção da força ao longo da linha Expresse o resultado como um vetor cartesiano.
Passo 1
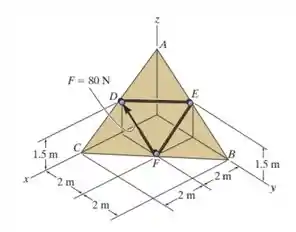
Fala galerinha bonita, tudo beleza?! Se liga só, nesse exercício aqui o enunciado nos deu uma força atuando em um sistema como no diagrama a seguir:
E sabendo disso, ele nos pede para encontrar os valores da projeção da força sobre a linha de .
Mas calma lá meu patrão, vamos com calma. Primeiro de tudo, a gente tem que a linha de atuação da força está em , ou seja, a linha que liga os pontos e .
Esses pontos são dados como:
Isso quer dizer que o vetor diretor dessa linha vai ser dado como:
E seu vetor unitário vai ser:
E como a força de atua nesse sentido, teremos que a sua forma vetorial será dada como:
Logo:
Passo 2
Iradoso, agora a linha que queremos projetar a força vai ser dada pelo vetor:
Onde os pontos e serão:
Logo:
E seu vetor unitário vai ser dado como:
Passo 3
Belezoca, então se a gente quer projetar a força na linha , podemos aplicar a fórmula da projeção dada como:
Onde representa o produto interno entre a força e o vetor dado por:
E como o módulo do vetor unitário é , temos , de modo que:
E se a gente tirar o módulo dessa força, vamos obter que:
