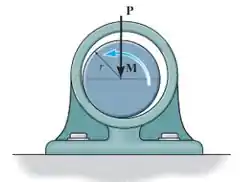
O eixo de raio se ajusta livremente no mancal radial. Se o eixo transmite uma força vertical ao mancal e o coeficiente e atrito cinético entre o eixo e o mancal é , determine o torque necessário para girar o eixo com velocidade constante.

Cara, temos um eixo dentro de um mancal e ele sofre uma força axial, que é transmitida ao mancal como uma força para baixo. A parada é que o mancal vai causar uma reação nesse cara, de mesmo módulo, para cima.

Mas essas forças não tem a mesma linha de ação, aí esse parzinho gera um momento dado pela fórmulinha:

Onde é a força de reação do mancal, lembra que ela tem o mesmo módulo da força transmitida pelo eixo? Então:

é o raio do eixo, e é o ângulo do coeficiente de atrito cinético.

Como ele quer o momento para girar esse eixo com velocidade constante, ele quer uma situação em equilíbrio.

Se a gente tem dois momentos atuando no eixo, esse gerado pelo par de forcinhas e o momento que o enunciado pede , a gente pode fazer o somatório de momentos no eixo:

Então o momento que a gente quer é dado por

Só falta achar quem é esse seno aí, e é vitória!