Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 122
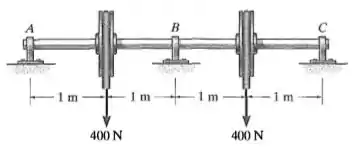
Determine as reações nos apoios de mancal , e do eixo; a seguir, trace os diagramas de força cortante e momento fletor. é constante. Cada mancal exerce somente reações verticais sobre o eixo.
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio e os diagramas. A dificuldade está em encontrar as reações de apoio, pois é uma estrutura hiperestática.
Como a gente tem três reações e só duas equações de equilíbrio para direção vertical, vamos começar substituindo um desses mancais por uma força. Aí teremos uma viga estaticamente equivalente.
Vamos fazer isso em , porque está no meio da viga, vai ajudar nas próximas continhas. Nossa viga nova fica assim:
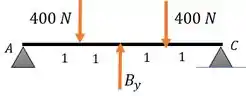
Aí a gente usa o conceito de linhas elásticas para achar mais uma equação com essas icógnitas. Por que? Cara, nesse ponto , na real, tem um apoio, isso quer dizer que a deflexão é zero nele:
Então a gente pode achar a expressão dessa deflexão e igualar a zero. Pronto, três equações e três icógnitas.
Bora seguir!
Passo 2
Agora vamos utilizar as equações de equilíbrio e momento para determinarmos as reações em função de :
Passo 3
Vamos achar a deflexão em . Podemos usar o método da superposição. Aí a gente usa o apêndice C para achar as fórmulinhas. Vamos separar nossa viga nessas situações:
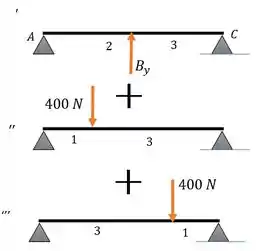
A fórmula para deflexão em para segunda viga (biapoiada com uma força concentrada ) é:
Onde é a distância da força até a extremidade mais próxima. E é a força. o comprimento total da viga.
Queremos o valor no meio da viga. Em . Por simetria, esse valor vai ser o mesmo para a terceira viga.
Para o primeiro caso (viga biapoiada com carga no meio), a fórmula de deflexão no meio é:
Pelo principio da superposição:
Passo 4
Essa deflexão precisa zerar porque na real nesse ponto há um apoio:
Substituindo nas equações obtidas anteriormente pelo equilíbrio, encontraremos as reações nos apoios restantes:
Passo 5
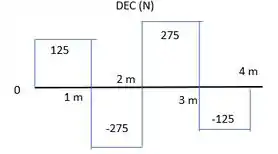
Agora, temos que esboçar os diagramas de força cortante e momento fletor. Para isso, temos:
Como só temos forças pontuais, desenhamos o diagrama do cortante seguindo a direção das forças. Em subimos , ficamos constantes até o primeiro .
Nele descemos e ficamos constantes até , onde a gente sobe o valor dessa força e fica constante até o segundo . Aí voltamos a descer esse valor e ficamos constantes até onde a gente sobe o valor dessa força. Ficamos assim:
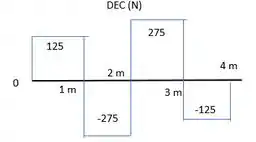
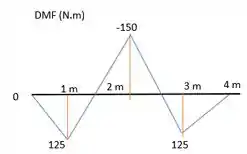
E para o momento a gente calcula os momentos em cada ponto onde há força, e liga esses pontos por retas. Fica assim:
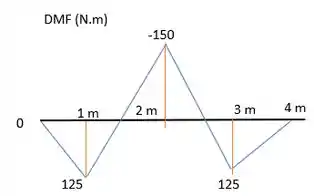
Resposta
